GIGANTY ŚWIATA 2D część 2
MODEL ŚWIATA PROSTOKĄTNEGO
Witam zainteresowanych tematem tworzenia gigantycznych światów 2D. Poniżej gigantyczny las w gigantycznym świecie- tylko fragment. Cały obszar to 2500×2500 kostek (kafli). Na tyle pozwolił mi mój komp
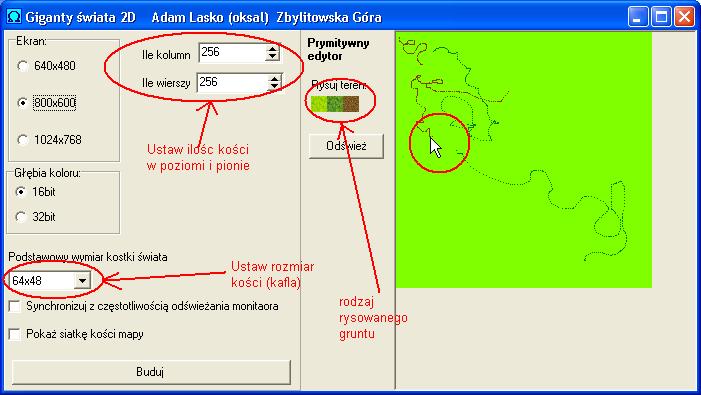
Strach się w nim zgubić, nie mówię o oprogramowaniu takiego poziomu gry…ale dla chcącego nic trudnego. W omawianym przykładzie drzewa są losowo sadzone w mapie warstwy pierwszej. Żeby nie było, że giganty to ściema utworzyłem prymitywny edytor, przy pomocy którego można sobie porysować po warstwie zerowej a potem odpalić program i dojść- przesunąć świat do wybranego punktu. Przesuwanie świata odbywa się „strzałkami”
Jak utworzyć GIGANTYCZNY ŚWIAT 2D?
Nie jest to trudne. Przypuśćmy chcemy mieć poziom gry w świecie 2500×2500 kafli dla każdej warstwy. Przyjmujemy, że warstw będzie trzy. Dla jednej warstwy da nam to
2500 razy 2500 = 6 250 000 kafli ,
dla trzech warstw będzie trzy razy tyle – 18 750 000 sztuk
Żadna gra 2D napisana w standardowy sposób nie pozwoli nam zagrać w takim świecie, będzie się dusić już dla świata 250 x 250.
Otóż standardowe tworzenie światów 2D polega na tym, że:
a) tworzy się tyle kafli ile jest w całym świecie
b) do każdego kafla przypisuje się grafikę
c) wyświetlane są tylko kafle widoczne
d) inne założenia o których nie wiem
Co należy zrobić?
Posłużę się takim porównaniem:
Siedzimy w czołgu, kończy nam się ostatnia skrzynka piwa (ja po skrzynkę amunicji bym nie pojechał- uraz dwa lata służby w drużynie łączności 1 komp. amunicyjnej, 5-tego samodzielnego batalionu zaopatrzenia przy 5 dywizji pancernej, dobrze ze była to drużyna łączności, łączność z piwem trwała bez większych zakłóceń) świat jaki widźmy jest ograniczony do PARU OBRAZÓW, drogę do piwa mamy w głowie- czyli MAPĘ. Nasza głowa pamięta obrazy jakie są przypisane do ścieżki dojścia do piwa…
Co z tego porównania wynika?
Jeżeli ekran komputera potraktujemy jako wizjer peryskopu a mapę wraz z informacjami o obrazach przelejemy z „głowy” do tablicy to możemy zbudować nowy model świata 2D- model GIGANTA
a) tworzymy tyle kafli ile mieści się w „wizjerze”
b) w mapie pamiętamy informacje o obrazach (konkretnie ich indeksy, pozostałe dane niesie ze sobą obraz, który jest załadowany w OmegaImageList)
c) tworzymy „nowy” sposób przesuwania świata oparty na czymś w rodzaju taśmociągu
I to jest z grubsza opisany cały pomysł. Teraz po kolei rozwinę podpunkty a, b i c
Ad a) tworzymy tyle kafli ile mieści się w „wizjerze”
Powiedzmy, że dla naszej gry ustalamy rozdzielczość 800×600 i podstawowy wymiar kości kafla na 64×48 pikseli. Z prostego rachunku wynika, że zmieści się nam
– w poziomie: 800 div 64 = 12 kafli
– w pionie : 600 div 48 = 12 kafli
Uzyskane wartości należy zwiększyć o 3 co da nam układ 15x 15. Czyli 225 kafli na warstwę. Jeżeli planujemy umieścić coś w rodzaju panelu gry na przykład u dołu ekranu. Powiedzmy o wysokości 96 pikseli pozwoli nam zmniejszyć ilość kafli w wierszach z 15 na 13. A więc w jednej warstwie będzie 15×13 = 195 kafli. Dla trzech warstw będzie to tylko 195 x 3 = 585 lub 225 x 3 = 675 (a to dużo mniej niż 6 250 000). I to nie zależnie czy świat będzie o rozmiarze 100 na 100 czy 2500 na 2500 . W moim modelu ważne jest aby nie budować światów mniejszych od granicznej ilości wyliczonej z przyjętej rozdzielczości i rozmiaru kafla.
Można zadać pytanie : Dlaczego zwiększamy rozmiar o 3?
Zwiększamy tylko ze względu na niepożądany efekt widoczności przerzucania obrazów w skrajnych kolumnach i wierszach. Skrajne kolumny i wiersze ustawiamy poza granicami ekranu monitora.
W artykułach o „Wędrówkach w świecie 2D” opisałem ze głębię kości (współrzędna Z) dobieram na podstawie numeru wiersza w którym dana kość się znajduje. Tu również to zastosowałem (patrz kod programu). W e wspomnianych artykułach opisałem powód takiego postepowania.
Ad b) w mapie pamiętamy informacje o obrazach (konkretnie ich indeksy, pozostałe dane niesie ze sobą obraz, który jest załadowany w OmegaImageList
Dla każdej warstwy tworzymy mapę świata. Czyli informację o indeksach użytych obrazów. I bardzo ważne jeżeli w danej komórce mapy świat nie istnieje obraz wstawiamy –1 (minus jeden). Co ten zabieg nam daje? Otóż nie będziemy rysować kafla który w danej chwili ma wartość indeksu obrazu ustawioną na minus jeden. Procedura DRAW kości warstwy nie będzie wykonana- zyskamy na prędkości gry.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
procedure TKostkaMapy.Draw; var Rect:TRect; begin if fSiatka then begin Image.Renderer.OmegaScreen.DrawRectangle(Round(x+1),Round(y+1),Round(x+DAneMApy.W1Kosc1), Round(y+DAneMApy.H1Kosc-1),false,1,125,125,125); exit; end; //nie rysuj jesli indeks wskazuje na -1 if (ImageIndex=-1)then exit; Image.Draw(Round(x+left),Round(y+top),0,0.5,0.5,1,1,Red,Green,Blue,Alpha,ImageIndex,0); end; |
Najczęściej takie pustostany występują w warstwie obiektów i gadżetów.
Ad c) tworzymy „nowy” sposób przesuwania świata oparty na czymś w rodzaju taśmociągu
Ten kto śledził ruch kości w programie dołączonym do części pierwszej, zauważył ze kość- kafel wykonuje ruch w ograniczonym obszarze. Jeżeli dojdzie do ustalonego punktu (patrz część pierwsza) to wraca na miejsce startu. Jest to bardzo ważna cecha mojego modelu- mogę powiedzieć rewolucyjna 🙂 Taki „kaczy” ruch wymaga zapamiętania współrzędnych punktu „uwięzienia” kafla. W kodzie programu pamiętają to zmienne x0, y0 każdej kości warstwy.
|
1 2 3 4 5 6 7 8 9 10 11 |
Indeks:=RogX+RogY*DaneMApy.XCount;//Pole mapy swiata x0:=a*DaneMapy.W1Kosc +RogSwiata.x;//przesun o poczatkowe polozenie rogu swiata y0:=b*DaneMapy.H1Kosc +RogSwiata.y;//przesun o poczatkowe polozenie rogu swiata dx:=0; dy:=0; |
Ale wracam do opisu …
Gdy pojedynczy kafel dojdzie do granicznego miejsca ma i musi (w woju było MAMUSI:) zostawić obraz i wrócić do współrzędnych startu x0, y0. Fakt zostawienia obrazu wiąże się z przekazaniem go sąsiadowi czy to lewemu, prawemu, górnemu lub dolnemu. To zależy w jakim kierunku przesuwamy świat. Przekazanie polega na przerzuceniu indeksu i kilku innych parametrów związanych na przykłada z kolorem (RGB) lub animacją. Zmiana ta wykonywana jest w
tej procedurze należącej do klasy bazowej utworzonych kafli
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
procedure TKostkaMapy.ZmianaKlatki; begin //jak w granicach świata to ustal indeks komórki w mapie świata if (RogX>-1)and(RogY>-1)and (RogX<danemapy.xcount)and(rogy<danemapy.ycount) <br=""> then Indeks:=RogX+RogY*DaneMApy.XCount else begin ImageIndex:=-1; exit;//wsykocz bo jeteś poza światem end; //załaduj nowy obraz i nową klatkę tego obrzau, odczytaną z mapy świata Image:=DaneMapy.OmegaImageList.ImageList.Items[Pmapa(Lista.Items[idWskMApy])^[indeks].idObrazka]; ImageIndex := PMapa(Lista.Items[idWskMApy])^[indeks].idKlatka; //uswta nowe wartości Red, Green, Blue, Alpha jakie niesie w sobie nowa komórka mapy świata RGBA; end; </danemapy.xcount)and(rogy<danemapy.ycount)> |
UWAGA:
Mapy warstw to tablice dynamiczne do których odwołuję się poprzez wskaźnik (patrz kod programu).
I to by było na tyle co do GIGANTÓW 2D w układzie prostokątnym . W następnej części opiszę GIGANTY IZOMETRYCZNE
Pozdrawiam oksal Zbylitowska Góra 8.01.2007
Autor: Oksal