GÓRY I DOLINY ŚWIATA 2D- część 1
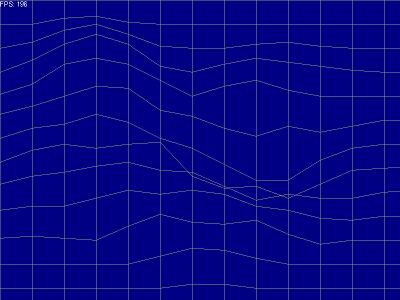
Cześć. Ten cykl jest próbą nowego podejścia do natury warstw świata 2D. Będziemy dążyć do takiego modelu jak na poniższym rysunku:
Tak, tak to jest OMEGA i DELPHI bez efektów 3D. Jak ja się cieszę, że C, C++ są kompilatorami o wysokich możliwościach, stąd też nie godne było dla nich stworzenie odpowiednika pakietu OMEGI. My gorsi PASCAL- owcy i DELPHI-arze musimy robić wszystko łatwiej, szybciej i przyjemniej…
1. ZAŁOŻENIA NOWEGO PODEJŚCIA DO WARSTW ŚWIATA 2D
a) Do prawidłowego działania gry 2D wystarczy jedna warstwa
b) Świat 2D nie musi być płaski
c) Warunki a i b powiązać z umiejętnościami nabytymi w klasycznym podejściu do problemu warstw świata 2D bez ingerencji w metody i rozwiązania 3D
Dlaczego nie musimy stosować kilku warstw?
Moim zdaniem da się napisać tak silnik 2D, że cała warstwa gruntu będzie osadzona w jednej siatce odpowiadającej warstwie 0 (zerowej). Elementy typu : budynki, drzewa, gadżety mogą być tak samo zorganizowane jak duszki bohaterów. Czyli być potomkami klasy TSprite, TSimpleAnimSprite lub mogą być wyświetlone jako rysunek bezpośrednio z OmegaImageList. Ale tu bym się wahał . Nie będziemy mieli łatwego dostępu do głębi, którą najłatwiej jest przechowywać w zmiennej Z. Głębię należy rozumieć tak jak ją opisałem w cyklu artykułów poświęconych Wędrówkom w świecie 2D. Klasy TSprite oraz TSimpleAnimSprite mają wbudowany efektywny mechanizm wykrywania kolizji. Choć można w przypadku budynków zastosować podejście takie jak do Karczmy opisanej w/ w cyklu artykułów. Szukanie drogi czy sprawdzanie możliwości ruchu duszka gracza a zwłaszcza duszków poruszających się automatycznie nie odbywa się po teście kolizji lecz po sprawdzeniu możliwości ruch w siatce warstwy. Należy pamiętać, że wspomniany test kolizji działa poprawnie gdy obiekty są widoczne na ekranie. A to można wykorzystać do zbierania gadżetów. Stąd można wywnioskować, że gadżet wcale nie musi być zapisany na przykład w warstwie 2 (drugiej). Ruch gadżetów, budynków czy też roślin jest łatwy do oprogramowania. Po prostu należy w ich współrzędnych odnotować skok duszka gracza.
Co do warunku: b) Świat 2D nie musi być płaski.
Nie jest to trudne do napisania. Podam jeden z pomysłów (tak niektóre gatunki napojów dobrze służą, człowiek często osiąga warstwę 0, z której bardzo fajnie widać góry i doliny…) Pomysł polega na odwzorowaniu punktów wysokości dla współrzędnych X,Y. Czyli na początek musimy umieć stworzyć taką rzeźbę terenu.
Tworzymy góry i doliny…
Efekt działania kodu części pierwszej
Oczywiście kod pozwala nam modelować rzeźbę terenu. Kształt rzeźby wywołujemy tym fragmentem kodu:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
procedure TForm1.FormMouseDown(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X, Y: Integer); begin ... ... .... //szczyty i doliny if Button=mbLeft then szczyt(idAktywny,-8); if Button=mbRight then szczyt(idAktywny, 8); end; |
Czyli kliknięcie lewym klawiszem myszy podnosi nam teren, prawy go obniża. Tu proszę się nie zmylić wartością -8 (minus osiem) podawaną do procedury szczyt gdy robimy góry. Lewy górny róg ekranu monitora ma współrzędne 0,0, dolny lewy będzie mieć 0,600 (przy rozdzielczości 800×600). Tak więc chcąc coś podwyższyć to musimy odjąć, obniżyć to dodać….
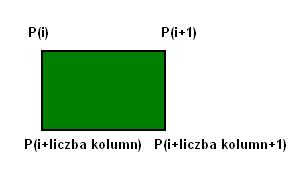
Na czym polega idea pomysłu? Najlepiej objaśnię to tym rysunkiem: 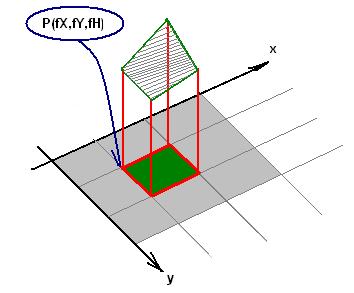
Kafel świata 2D jest prostokątem. Dla każdego rogu kafla oprócz współrzędnej X,Y musimy zapamiętać poziom wysokości H. W przypadku modelowania rzeźby terenu musimy mieć możliwość jej zmiany. Gdy będzie to już gra, to taka zmiana nie jest konieczna. Dane terenu będą ładowane z pliku. Współczynnik FPS nam wzrośnie. Edytor zawsze cechuje się mniejszym FPS-em. Ponieważ musimy na bieżąco kontrolować zmiany różnych parametrów. A to wymaga dodatkowych obliczeń nie występujących w grze…
Ale wróćmy do sedna sprawy…Mając zbiór punktów P(fX,fY,fH) jesteśmy wstanie odwzorować góry i doliny w świecie 2D. Pojedynczy kafel będzie oparty na zbiorze współrzędnych :
P(i),
P(i+1),
P(i+ liczba kolumn),
P(i+ liczba kolumn+1)
Wartości w nawiasach są indeksami punktów przechowywanych w tablicy lub w liście wskaźników. Ja w tym rozwiązaniu zastosuje wskaźniki. A to z tego względu, że wskaźnik jest bardziej efektywny, mniej obciąża pamięć i dostęp jest szybszy. Może tu jedynie kogoś zniechęcić używanie w indeksach punktu P jakiś dodatkowych przesunięć. Przesunięcia te są konsekwencją takiego podejścia: mamy 100 elementów zapisanych w liście jednokierunkowej od 0 do 99 indeksu. Jeżeli teraz chcielibyśmy umieścić te elementy w tablicy 10×10, to otrzymamy taki zapis indeksów ( ważne przeczytaj tekst objaśniający zapisany na poniższym rysunku):
No i pewnie ktoś w tym miejscu powie po co sobie utrudniać życie organizując zapis tak jak byśmy wieszali korale na nici, przecież można to zrobić w tablicy i problemy zniknie. Tak to prawda. Ale Delphi ma wspaniały mechanizm list jednokierunkowych przechowujących wskaźniki. Bezwiednie na pewno czytelniku z tego korzystałeś. Chociażby komponentey TListBox, TMemo…
Ja zastosuję TList . Tu można łatwo dodawać, usuwać, filtrować, sortować itp. Więcej informacji znajdziesz w pomocy do Delphi
Jak zorganizować przechowywanie informacji o rzeźbie terenu?
Rzeźba terenu to zbiór punktów pamiętających współrzędne i wysokość. Zbudujemy więc klasę przeznaczoną do przechowywania tych informacji wraz z możliwością ich zmiany oraz rysującą punkty i linie połączeń między punktami. Postać wspomnianej klasy
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
PPunkt=^TPunkt; TPunkt=class fOmegaPrimitives:TOmegaPrimitives; fOmegaScreen:TOmegaScreen; fX, //współrzędna X fY :single; //współrzędna Y fZ :integer;//współrzędna Z fH :single;//poziom wysokości fRed, fGreen, fBlue :integer; protected property X:single read fX write fX; property Y:single read fY write fY; property Z:integer read fZ write fZ; property H:single read fH write fH; property Red :integer read fRed write fRed; property Green :integer read fGreen write fGreen; property Blue :integer read fBlue write fBlue; public procedure Draw(const Xk,Yk,XKPion,YKPion:single); constructor Create(const AX,AY:single;const AZ:integer; const AR,AG,AB:integer; const AOmegaScreen:TOmegaScreen); end; |
Myślę, że przeznaczenie zmiennych jest jasne. Co prawda nie wykorzystuję zmiennej fZ ale na wszelki wypadek ją wprowadzę. Może w późniejszych rozwiązaniach się przyda. W klasie TPunkt znajduje się takie pole : fOmegaPrimitives: TOmegaPrimitives ; To pole ma metody związane z rysowaniem linii, okręgów itp Nam się przyda do linii. Czyli wizualizacji siatki terenu. Procedury Draw i Create są bardzo proste w zrozumieniu. Wystarczy spojrzeć do kodu.
Dla osób nigdy nie wykorzystujących list wskaźnikowych omówię pokrótce zasadę jej tworzenia.
W części var należy zadeklarować taką listę
|
1 2 3 |
var Lista:Tlist; |
a następnie ją utworzyć. Najwygodniej jest to zrobić tak jak poniżej
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
procedure TForm1.FormCreate(Sender: TObject); begin Lista:=TList.Create; TworzPunkty(0,0); ......... .......... end; |
Dodanie punktów do listy zrobimy w procedurze TworzPunkty(const RogX,RogY:integer). Parametry RogX, RogY to wartości zaczepienia pierwszego punktu w układzie współrzędnych ekranu. Postać tej procedury jest bardzo prosta
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
procedure TworzPunkty(const RogX,RogY:integer); var w,k:integer; APunkt:PPunkt; begin for w:=0 to SiatkaMapy.y-1 do for k:=0 to SiatkaMapy.x-1 do begin New(APunkt); APunkt^:=TPunkt.Create(RogX+k*RozmiarKfla.x,RogY+w*RozmiarKfla.y,0,0,255,0,Form1.OmegaScreen1); Lista.Add(APunkt); end; end; |
Jak widać lista wskaźników w Delphi nie powstaje w bólach. Należy jeszcze pamiętać o zwolnieniu pamięci po zakończeni działania programu. Czyli robimy to tak:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
procedure TForm1.FormDestroy(Sender: TObject); var i:integer; begin for i:=0 to Lista.Count-1 do Dispose(PPunkt(Lista.Items)); Lista.Free; end; |
Podam jeszcze w jaki sposób można odczytać na przykład współrzędną fX powiedzmy dwunastego elementu z listy:
|
1 |
....:=PPunkt(Lista.Items[12])^.fX; |
Proste i eleganckie (i w ogóle mnie to nie interesuje jak to się robi w C, w WC to, to się olewa:). Wiem już jak tworzyć zbiór punktów teraz przeanalizujemy budowę szczytów i dolin.
Szczyty
W omawianym kodzie tworzenie gór i dolin zajmuje się jedna i ta sam procedura
|
1 |
procedure szczyt(const n:integer;const h:single); |
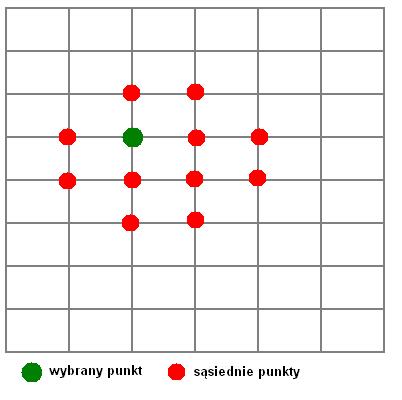
gdzie n to indeks wybranego punktu a h to współczynnik wzniosu lub pochyłości. Przy budowie wypukłości posłużyłem się czymś w rodzaju „pędzla” zwiększającego współczynnik wysokości ograniczonego obszaru, który znajduje się w sąsiedztwie wybranego punktu. Najlepiej przedstawię to rysunkami.
„Pędzel” wybiera punkty do obróbki według zasady przedstawionej na rysunku
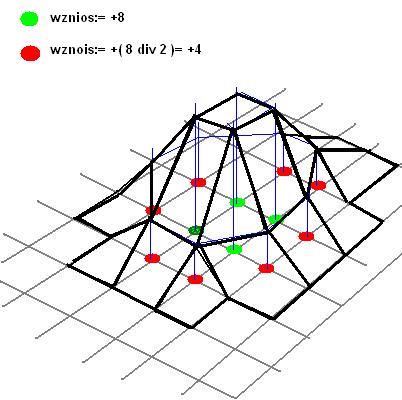
po zadziałaniu procedury Szczyt otrzymamy coś takiego
Aktualny pędzel podnosi jednego kafla i modyfikuje rogi sąsiednim kafla. Można sobie przygotować kilka pędzli do tworzenia płaskowyżów lub obszarów przeznaczonych pod budynki. W omawianym rozwiązaniu kłopotliwe jest wyznaczenie rogów sąsiednich kafli. Ja zdecydowałem się na układ wybierania oparty na tablicy skoków po indeksach. Poniżej ją przytoczę:
|
1 |
pedzel0:array[0..11,0..1]of integer=((0,0),(1,0),(1,1),(0,1),(0,-1),(1,-1),(2,0),(2,1),(1,2),(0,2),(-1,1),(-1,0)); |
Kod procedury Szczyt:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
procedure szczyt(const n:integer;const h:single); var wiersz,kol,i,j:integer; begin if n=0 then exit; wiersz:=n div SiatkaMapy.x; kol:=n-wiersz*siatkaMapy.x; for i:=0 to high(pedzel0) do if kol+pedzel0[i,0] begin j:=kol+pedzel0[i,0]+(wiersz+pedzel0[i,1])*siatkaMapy.x; if (j>-1)and(j<lista.count)then <br=""> begin if i<4 then PPunkt(Lista.items[j])^.fh:=PPunkt(Lista.items[j])^.fh+h else PPunkt(Lista.items[j])^.fh:=PPunkt(Lista.items[j])^.fh+h/2; end; end; end;</lista.count)then> |
Zostawiam Tobie czytelniku do przeanalizowania.
Linie siatki i obrazy punktów możemy pokazać lub ukryć jeżeli wybierzemy z klawiatury:
-klawisz SPACJA- pokaż/ ukryj siatkę
-klawisz P- pokaż/ ukryj punkty
I to tyle w części pierwszej. W części drugiej omówię sposób deformacji bitmapy kafla oraz uzyskanie efektu cieniowania kafla. Proszę się nie przerażać. W OMEDZE nie jest to trudno zrobić. Klasa TIamgeList posiada pewną funkcję która zrobi to za jednym zamachem. Tworząc efekt taki jak na pierwszym rysunku tego artykułu. Wystarczy tylko zmodyfikować procedurę Draw duszka kafla. Ale o tej funkcji- Draw4Col będzie w następnej części.
Pozdrawiam oksal Zbylitowska Góra 20.07.2006
Autor: oksal