Jak znaleźć najkrótszą drogę do celu w świecie 2D? - Unit1.pl - Programowanie

JAK ZNALEŹĆ NAJKRÓTSZĄ DROGĘ DO CELU W ŚWIECIE 2D?

Prawdopodobnie ten artykuł nie będzie zbyt oryginalny co do użytego algorytmu określającego drogę dojścia do celu. Sposób znalezienia szlaku oparłem na algorytmie Dijkstry oraz opracowaniu jakie można znaleźć w książce „Algorytmy” Macieja Sysło. Książka ta jest doskonałym uzupełnieniem podręcznika do informatyki w szkole średniej tegoż autora (tytuł podręcznika to „Informatyka” część 2-ga). W internecie można znaleźć kilka opracowań tego algorytmu. W tej chwili nie potrafię wskazać konkretnych adresów ale przypominam sobie, że widziałem opracowania omawianego problemu na stronach Politechniki Poznańskiej. Różnice są, ale wynikają one ze sposobu „oprogramowania” problemu.

Ja w swoim rozwiązaniu nie używam grafów oraz rekurencji. Ponadto funkcję oparłem na tablicy dynamicznej. Co pozwala ją zastosować do różnych wielkości światów 2D. Wyniki czasowe jakie uzyskuję są bardzo zadawalające. Poniżej przytoczę kilka z nich:
Ilość kolumn świata 2DIlość wierszy świata 2DCzas
256256Średnio 20 – 60 ms
512512W granicach 100 ms
10241024W granicach 500 ms

Sprzęt jaki posiadam nie jest rewelacyjny. Procesor to Duron 850 MHz i 512 MB RAM-u. Proszę popatrzeć dla mapy świata 1024×1024 czas określenia drogi jest rzędu połowy jednej sekundy. Zaś dla świata w układzie 256×256 to już 20-60 milisekund. Tu chce podkreślić że testy przeprowadzałem dla określenia drogi po przekątnej mapy świata . Czyli z górnego lewego rogu do dolnego prawego rogu. Teoretycznie najbardziej odległe punkty. Układ świat dobierałem na drodze losowej.

Postać algorytmu

Podaję za autorem książki „Algorytmy” Maciejem Sysło

Dane: Labirynt (u nas mapa świata 2D, czyli prostokąt z jednym wyjściem, wypełniony ścianami, które są równoległe do zewnętrznych ścian i nie tworzą zamkniętych obszarów. Dany jest punkt w polu s (nasz punkt startu)
Wynik: Droga w labiryncie, która prowadzi z pola s do wyjścia
Krok 0: Przyjmij, ze na początku nie byłeś w żadnym polu labiryntu, a więc wszystkie pola są nieodwiedzone.
Krok 1: Umieść w kolejce Q pole s. W polu s umieść liczbę 0 (zero).
Krok 2: Dopóki kolejka Q nie jest pusta wykonuj kroki 3- 5
Krok 3: Usuń z kolejki Q jej pierwszy element – oznaczmy to pole przez v
Krok 4: Dla każdego pola w sąsiedniego względem v i nie oddzielonego od niego ścianą wykonaj krok 5
Krok 5: Jeśli nie byłeś jeszcze w polu w, to umieść w nim liczbę o jeden wiesza od liczby znajdującej się w polu v. Jeśli pole w zawiera wyjście to przejdź do kroku 6, a w przeciwnym razie dołącz w do końca kolejki Q
Krok 6: {W tym kroku budujemy od końca listę pól tworzących najkrótszą drogę z pola s do pola w, na którym zakończył działanie krok 5}
Dopóki w nie jest polem s, wykonuj: za kolejne (od końca) pole drogi przyjmij w i za nową wartość w przyjmij sąsiednie względem w, w którym znajduje się liczba o jeden mniejsza od liczby znajdującej się w obecnym polu w.

Oczywiście na potrzeby gry algorytm trzeba zmodyfikować tak aby dana jednostka mogła podejść do wybranego punktu możliwie najbliżej w przypadku gdy drogi dojścia do celu nie będzie. Kiedy taka sytuacja może nastąpić? Na przykład jednostki wroga są ukryte za gęstym lasem lub rzeką. Moja funkcja to uwzględnia. Wystarczy podczas testów narysować mur jedynek…

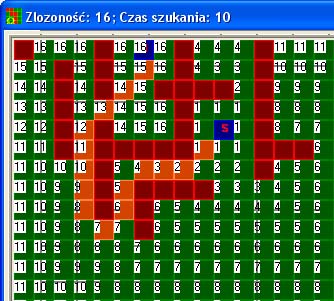
Ale wróćmy do tematu… Przedstawiony algorytm można zobrazować poniższym rysunkiem

Rozwiązanie

Można powiedzieć, że ten artykuł jest swoistą kontynuacją wątku zaproponowanego przez Tostera https://kompendium.unit1.pl/forum/viewtopic.php?t=644 Stąd też ciało mojej funkcji ukryję w bibliotece dołączonej do artykułu (plik oksalDijkstra.dll) a w załączonym kodzie programu testowego pokażę i opiszę jak tą funkcję wykorzystać we własnych projektach. Oczywiście jeżeli czytelniku uda Ci się tak oprogramować problem, że wyniki czasowe będą lepsze to namawiam do podzielenia się Twoją funkcją.

W pliku Dijkstra.pas jest to co nas interesuje.

function NajkrotszaDroga(const ASwiat:TSwiat;
                         const AStart,ACel:TPoint;
                         const AKolumny,AWiersze:integer;
                         var ADroga:PDroga):boolean;StdCall;

function NajkrotszaDroga(const ASwiat:TSwiat;

const AStart,ACel:TPoint;

const AKolumny,AWiersze:integer;

var ADroga:PDroga):boolean;StdCall;

Jeżeli będziesz chciał tą funkcje wykorzystać to musisz ja wywołać w swoim projekcie poniższą konstrukcja:

implementation
uses Dijkstra;

1 2	implementation uses Dijkstra;

Przytoczona funkcja wymaga sześciu parametrów. Poniżej kolejno je omówię:

1) const ASwiat:Tswiat – spełnia rolę siatki mapy, TSwiat należy rozumieć jako tablicę dynamiczną

TSwiat=array of array of integer;

1	TSwiat=array of array of integer;

która wypełniamy podczas ładowania mapy gry. Na potrzeby artykułu ja zrobiłem to w ten sposób

setLength(Swiat,wiersze,kolumny);
 for i:=0 to Memo1.Lines.Count-1 do begin
     for j:=1 to length(Memo1.Lines.Strings[i])do
     if Memo1.Lines.Strings[i][j]='0'then
     Swiat[i,j-1]:=0 else Swiat[i,j-1]:=1;
 end;

setLength(Swiat,wiersze,kolumny);

for i:=0 to Memo1.Lines.Count-1 do begin

for j:=1 to length(Memo1.Lines.Strings[i])do

if Memo1.Lines.Strings[i][j]='0'then

Swiat[i,j-1]:=0 else Swiat[i,j-1]:=1;

end;

Tablica typu TSwiat jest zorganizowana w układzie wiersz – kolumna. To znaczy zapis Swiat[i,j] należy rozumieć tak: symbol i to indeks wiersza, j to indeks kolumny.

Uwaga: wartość 0 (zero) oznacza, że jest wolna droga, 1 (jeden) – przejście zabronione. Tu pewnie ktoś może powiedzieć, że w rzeczywistej grze liczba klatek obrazów kafli możliwych do przejścia jest znaczna ilość, a ja proponuję użycie tylko dwóch indeksów 0 i 1. To podejście jest podyktowane szybkością wykonywania testów przejścia.

Powstaje pytanie: Jak zwiększyć liczbę możliwych klatek przejścia?

Najłatwiej jest przygotować sobie tablicę indeksów obrazów kafli po których można chodzić i w momencie ładowania mapy gry sprawdzać czy ładowny indeks należy do takiego zbioru. Jeżeli tak to wstaw zero w przeciwnym wypadku wstaw jeden do tablicy Swiat[i,j]. Nic nie tracimy na czasie bo ładowanie siatek gry odbywa się na początku. Ewentualne zmiany można nanosić podczas trwania gry, na przykład gdy przeciwnik wzniósł mur obronny.

2) const AStart,ACel:Tpoint – to współrzędne indeksów pól startu i celu wybranych na siatce mapy świata 2D, które w programie na potrzeby artykułu wypełniłem tak:

Start.x:=0;
Start.y:=0;
Cel.x:=kolumny-1;
Cel.y:=wiersze-1;

Start.x:=0;

Start.y:=0;

Cel.x:=kolumny-1;

Cel.y:=wiersze-1;

2) const AKolumny,AWiersze:integer – są to wartości określające liczbę kolumn i wierszy siatki mapy świata 2D. Wartości tych parametry mogą być dowolne (oczywiście w zakresie wytrzymałości pamięci i przypisanych zakresów , tu Integer)

3) var ADroga:PDroga – to tablica wyznaczonej drogi, jest to konkretnie wskaźnik na tablicę dynamiczną. Jej deklaracja poniżej

type
  TWspolrzedna=record
       wiersz:longInt;
       kolumna:longInt;
       end;

  PDroga=^TDroga;
  TDroga=array of TWspolrzedna;

  TSwiat=array of array of integer;

Var

Droga:PDroga;//Tablica kolejnych kafli tworzących ścieżkę znalezionej drogi

type

TWspolrzedna=record

wiersz:longInt;

kolumna:longInt;

end;

PDroga=^TDroga;

TDroga=array of TWspolrzedna;

TSwiat=array of array of integer;

Var

Droga:PDroga;//Tablica kolejnych kafli tworzących ścieżkę znalezionej drogi

I to tyle na temat opisu parametrów podawanych do funkcji. Użycie samej funkcji jest proste

procedure TForm1.Button5Click(Sender: TObject);
var
 wynik:boolean;
 czas0,czas1:LongInt;
 Start,Cel:TPoint;
 j:LongInt;
begin
 Start.x:=0;
 Start.y:=0;
 Cel.x:=kolumny-1;
 Cel.y:=wiersze-1;

 czas0:=GetTickCount;

 Droga:=nil;
 wynik:=NajkrotszaDroga(Swiat,Start,Cel,Kolumny,wiersze,Droga);

 czas1:=GetTickCount;

 Memo2.Lines.Clear;
 if not wynik then
    MessageBox(handle,'Nie można dojść do wyznaczonego punktu'
                      +#13#10'Doszedłem możliwie najbliżej' ,'komunikat',mb_ok);
.....

procedure TForm1.Button5Click(Sender: TObject);

var

wynik:boolean;

czas0,czas1:LongInt;

Start,Cel:TPoint;

j:LongInt;

begin

Start.x:=0;

Start.y:=0;

Cel.x:=kolumny-1;

Cel.y:=wiersze-1;

czas0:=GetTickCount;

Droga:=nil;

wynik:=NajkrotszaDroga(Swiat,Start,Cel,Kolumny,wiersze,Droga);

czas1:=GetTickCount;

Memo2.Lines.Clear;

if not wynik then

MessageBox(handle,'Nie można dojść do wyznaczonego punktu'

+#13#10'Doszedłem możliwie najbliżej' ,'komunikat',mb_ok);

.....

Jeżeli nie można dojść do celu to zostanie zwrócona przez omawianą funkcję wartość false. Co również można w grze wykorzystać.

Uwagi do testowania

Program pozwala generować losowe układy map o zadanej liczbie kolumn w tych zmiennych

const
  kolumny=256;//512;//1024;//liczone od 1
  wiersze=256;//512;//1024;//liczone od 1

const

kolumny=256;//512;//1024;//liczone od 1

wiersze=256;//512;//1024;//liczone od 1

Wygenerowany układ można zapisać w pliku tekstowym. Jeżeli nie chcemy mieć losowego układu to należy wygenerować pusty świat używając klawisza „Generuj puste”, zapisać wynik do pliku i na przykład w notatniku pozamieniać zera na jedynki- czyli „narysować” przeszkody. Odszukana tablica drogi jest przedstawiana w formie tekstowej jak i graficznej- należy przejść na odpowiednią zakładkę. I tu uwaga: ja zastosowałam statyczny obraz siatki mapy świata 2D w układzie 256×256 w postaci bitmapy i jeżeli będziemy testować światy o większej liczbie kolumn i wierszy to ze zrozumiałych względów pola powyżej zakresu 256 nie będą widoczne. Tablica drogi będzie wyznaczona poprawnie.

Do przykładu dołączam kilka plików tekstowych wygenerowanych światów które można załadować do działającej aplikacji.

I to by było na tyle

Pozdrawiam
Oksal

Zbylitowska Góra 24.08.2006

Dodane:

Otwarty kod funkcji podającej tablicę drogi

function NajkrotszaDroga(const ASwiat:TSwiat;
                          const AStart,ACel:TPoint;
                          const AKolumny,AWiersze:integer;
                          var ADroga:PDroga):boolean;
const                              //  k,w     k,w    k,w
 kierunek:array[0..7,0..1]of integer=((0,-1),(1,0),(0,1),(-1,0),(-1,-1),(1,-1),(1,1),(-1,1));
var
 fWynik,
 fMeta:boolean;
 row,
 col,
 Zalazek,
 j,k,L:LongInt;
 rozmiarBufora:LongInt;
 tabKolejka  :array of TWspolrzedna;
 tabBufor    :array of TWspolrzedna;
 _Cel:TPoint;
 ileOdwiedzin:array of array of LongInt;
 tabodwiedzin:array of array of boolean;
 odleglosc:extended;
 zlozonosc,
 i,WxK,
 MaxIndeks:int64;
begin
 odleglosc:=High(dWord);
 MaxIndeks:=0;
 zlozonosc:=0;
 fWynik:=true;
 fMeta:=false;
 setLength(ileOdwiedzin,AWiersze,AKolumny);
 setLength(tabodwiedzin,AWiersze,AKolumny);
 //Utworz rozmiar pocztakowy tablicy kolejka
 setLength(tabKolejka,1);
 //zapamietaj pozycje startu
 // _start:=Astart;
 tabKolejka[0].wiersz :=Astart.y;
 tabKolejka[0].kolumna:=Astart.x;
 tabOdwiedzin[tabKolejka[0].wiersz,tabKolejka[0].kolumna]:=true;
//romiar poczatkowy tablicy bufora
 rozmiarBufora:=1;
 _Cel:=Acel;//w y jest wiersz w x jest kolumna startu
 WxK:=AWiersze*AKolumny-1;
 while (not fMeta) do
 begin
  //Kolejka
  for j:=0 to high(tabKolejka)do
  begin
    //pętal dla 4 lub 8 kierunków szukania drogi
    for k:=0 to high(kierunek) do
    begin
     col:=tabKolejka[j].kolumna+kierunek[k,0];
     row:=tabKolejka[j].wiersz+kierunek[k,1];
     if (col<0)or(col>=AKolumny)or(row<0)or(row>=AWiersze)then continue;
     if(ASwiat[row,col]=0)
     then
     begin
       if tabOdwiedzin[row,col]=false then begin
          ileOdwiedzin[row,col]:=ileOdwiedzin[tabKolejka[j].wiersz,tabKolejka[j].kolumna]+1;
          tabOdwiedzin[row,col]:=true;
          setlength(tabBufor,rozmiarBufora);
          tabBufor[rozmiarBufora-1].wiersz:=row;
          tabBufor[rozmiarBufora-1].kolumna:=col;
          inc(rozmiarBufora);
          //if (odleglosc>=Abs(WagaMety-col-row*AKolumny))then
          if (odleglosc>=sqrt(sqr(_Cel.y-row)+sqr(_Cel.x-col))) then
              begin
              odleglosc:=sqrt(sqr(_Cel.y-row)+sqr(_Cel.x-col));
              MaxIndeks:=col+row*AKolumny;
              end;
          if (col=_Cel.x)and(row=_Cel.y)then begin
             fMeta:=true;
             break;
          end;
       end;
     end;
    end;//koniec petli dla kierunkow
   end;//koniec petli dla biezacej kolejki
  //zniszcz koljekę
  tabKolejka:=nil;
  setLength(tabKolejka,high(tabBufor)+1);
  //zapamietaj nowa kolejkę
  for k:=0 to high(tabBufor)do tabKolejka[k]:=tabBufor[k];
  //zniszcz bufor
  tabBufor:=nil;
  rozmiarBufora:=1;
  inc(zlozonosc);
  if zlozonosc>WxK then
    begin
     //nie znaleziono drogi, wiec podejdz najblizej do celu
     _Cel.Y:=Maxindeks div AKolumny;
     _Cel.X:=Maxindeks-_Cel.Y*Akolumny;
     fWynik:=false;
     fMeta:=true;
     break;
    end;
 end;{koniec while}
 //***********************************************
 Zalazek:=ileOdwiedzin[_Cel.y,_Cel.x];
 rozmiarBufora:=1;
 Setlength(tabKolejka,rozmiarBufora);
 
 Setlength(ADroga^,rozmiarBufora);
 
 TabKolejka[0].wiersz:=_Cel.y;
 TabKolejka[0].kolumna:=_Cel.x;
 
 ADroga^[0].wiersz:=TabKolejka[0].wiersz;
 ADroga^[0].kolumna:=TabKolejka[0].kolumna;
 fmeta:=false;
 i:=0;
 while i<zlozonosc do
 begin
   for k:=0 to high(kierunek) do
   begin
    col:=TabKolejka[high(TabKolejka)].kolumna+kierunek[k,0];
    row:=TabKolejka[high(TabKolejka)].wiersz+kierunek[k,1];
    if (col<0)or(col>=AKolumny)or(row<0)or(row>=AWiersze)then continue;
    if(ASwiat[row,col]=0)
    then begin
      if ileOdwiedzin[row,col]=Zalazek-1then
      begin
         Zalazek:=ileOdwiedzin[row,col];
         inc(rozmiarBufora);
         Setlength(tabKolejka,rozmiarBufora);
         TabKolejka[high(TabKolejka)].kolumna:=col;
         TabKolejka[high(TabKolejka)].wiersz:=row;
         Setlength(ADroga^,rozmiarBufora);
         ADroga^[high(TabKolejka)].wiersz :=TabKolejka[high(TabKolejka)].wiersz;
         ADroga^[high(TabKolejka)].kolumna:=TabKolejka[high(TabKolejka)].kolumna;
         if(col=Astart.x)and(row=Astart.y)then i:=zlozonosc;//fMeta:=true;
         break;
      end;//Koniec szukania zalazka
    end;//konec testu komorek tablicy
   end;//koniec kierunku
   //
   inc(i);
  end;//koniec while
  result:=fWynik;
end;

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

function NajkrotszaDroga(const ASwiat:TSwiat;

const AStart,ACel:TPoint;

const AKolumny,AWiersze:integer;

var ADroga:PDroga):boolean;

const // k,w k,w k,w

kierunek:array[0..7,0..1]of integer=((0,-1),(1,0),(0,1),(-1,0),(-1,-1),(1,-1),(1,1),(-1,1));

var

fWynik,

fMeta:boolean;

row,

col,

Zalazek,

j,k,L:LongInt;

rozmiarBufora:LongInt;

tabKolejka :array of TWspolrzedna;

tabBufor :array of TWspolrzedna;

_Cel:TPoint;

ileOdwiedzin:array of array of LongInt;

tabodwiedzin:array of array of boolean;

odleglosc:extended;

zlozonosc,

i,WxK,

MaxIndeks:int64;

begin

odleglosc:=High(dWord);

MaxIndeks:=0;

zlozonosc:=0;

fWynik:=true;

fMeta:=false;

setLength(ileOdwiedzin,AWiersze,AKolumny);

setLength(tabodwiedzin,AWiersze,AKolumny);

//Utworz rozmiar pocztakowy tablicy kolejka

setLength(tabKolejka,1);

//zapamietaj pozycje startu

// _start:=Astart;

tabKolejka[0].wiersz :=Astart.y;

tabKolejka[0].kolumna:=Astart.x;

tabOdwiedzin[tabKolejka[0].wiersz,tabKolejka[0].kolumna]:=true;

//romiar poczatkowy tablicy bufora

rozmiarBufora:=1;

_Cel:=Acel;//w y jest wiersz w x jest kolumna startu

WxK:=AWiersze*AKolumny-1;

while (not fMeta) do

begin

//Kolejka

for j:=0 to high(tabKolejka)do

begin

//pętal dla 4 lub 8 kierunków szukania drogi

for k:=0 to high(kierunek) do

begin

col:=tabKolejka[j].kolumna+kierunek[k,0];

row:=tabKolejka[j].wiersz+kierunek[k,1];

if (col<0)or(col>=AKolumny)or(row<0)or(row>=AWiersze)then continue;

if(ASwiat[row,col]=0)

then

begin

if tabOdwiedzin[row,col]=false then begin

ileOdwiedzin[row,col]:=ileOdwiedzin[tabKolejka[j].wiersz,tabKolejka[j].kolumna]+1;

tabOdwiedzin[row,col]:=true;

setlength(tabBufor,rozmiarBufora);

tabBufor[rozmiarBufora-1].wiersz:=row;

tabBufor[rozmiarBufora-1].kolumna:=col;

inc(rozmiarBufora);

//if (odleglosc>=Abs(WagaMety-col-row*AKolumny))then

if (odleglosc>=sqrt(sqr(_Cel.y-row)+sqr(_Cel.x-col))) then

begin

odleglosc:=sqrt(sqr(_Cel.y-row)+sqr(_Cel.x-col));

MaxIndeks:=col+row*AKolumny;

end;

if (col=_Cel.x)and(row=_Cel.y)then begin

fMeta:=true;

break;

end;

end;//koniec petli dla kierunkow

end;//koniec petli dla biezacej kolejki

//zniszcz koljekę

tabKolejka:=nil;

setLength(tabKolejka,high(tabBufor)+1);

//zapamietaj nowa kolejkę

for k:=0 to high(tabBufor)do tabKolejka[k]:=tabBufor[k];

//zniszcz bufor

tabBufor:=nil;

rozmiarBufora:=1;

inc(zlozonosc);

if zlozonosc>WxK then

begin

//nie znaleziono drogi, wiec podejdz najblizej do celu

_Cel.Y:=Maxindeks div AKolumny;

_Cel.X:=Maxindeks-_Cel.Y*Akolumny;

fWynik:=false;

fMeta:=true;

break;

end;

end;{koniec while}

//***********************************************

Zalazek:=ileOdwiedzin[_Cel.y,_Cel.x];

rozmiarBufora:=1;

Setlength(tabKolejka,rozmiarBufora);

Setlength(ADroga^,rozmiarBufora);

TabKolejka[0].wiersz:=_Cel.y;

TabKolejka[0].kolumna:=_Cel.x;

ADroga^[0].wiersz:=TabKolejka[0].wiersz;

ADroga^[0].kolumna:=TabKolejka[0].kolumna;

fmeta:=false;

i:=0;

while i<zlozonosc do

begin

for k:=0 to high(kierunek) do

begin

col:=TabKolejka[high(TabKolejka)].kolumna+kierunek[k,0];

row:=TabKolejka[high(TabKolejka)].wiersz+kierunek[k,1];

if (col<0)or(col>=AKolumny)or(row<0)or(row>=AWiersze)then continue;

if(ASwiat[row,col]=0)

then begin

if ileOdwiedzin[row,col]=Zalazek-1then

begin

Zalazek:=ileOdwiedzin[row,col];

inc(rozmiarBufora);

Setlength(tabKolejka,rozmiarBufora);

TabKolejka[high(TabKolejka)].kolumna:=col;

TabKolejka[high(TabKolejka)].wiersz:=row;

Setlength(ADroga^,rozmiarBufora);

ADroga^[high(TabKolejka)].wiersz :=TabKolejka[high(TabKolejka)].wiersz;

ADroga^[high(TabKolejka)].kolumna:=TabKolejka[high(TabKolejka)].kolumna;

if(col=Astart.x)and(row=Astart.y)then i:=zlozonosc;//fMeta:=true;

break;

end;//Koniec szukania zalazka

end;//konec testu komorek tablicy

end;//koniec kierunku

inc(i);

end;//koniec while

result:=fWynik;

end;

Załączniki

droga
Rozmiar pliku: 85 KB

Załączniki

Artykuły powiązane

Muzyka trackerowa w grach casual.

Algorytm wyszukiwania najkrótszej drogi w świecie 2D

Small Games (paczki i mały exe)

Piszemy platformówkę część 2.

[Delphi] Save Game

Piszemy platformówkę część 1.