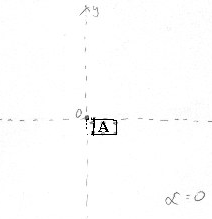
Dany jest obiekt A (rys.1).
Zadanie polega na obróceniu go wokół osi przechodzącej przez punkt O. Dane są współrzędne każdego piksela należącego do obiektu(x,y). Przedstawione rozwiązanie zakłada obliczanie współrzędnych dla punktów leżących na osi OX (odległość od punktu O jest równa x). Jak wynika z rysunku drugiego:
|
1 |
x1=cos(alfa)*x; y1=sin(alfa)*x; |
Te wzory nie pozwalają jednak na obliczenie współrzędnych punktów, które dla alfa=0, nie leżą na osi OX. Żeby obliczyć je należy przesunąć układ współrzędnych prostopadle do prostej tworzącej z osią OX kąt alfa o wartość y. Ostatecznie równania powinny wyglądać tak:
|
1 2 3 |
x1=cos(alfa)*x+cos(alfa+90)*y; y1=sin(alfa)*x+sin(alfa+90)*y; |
W programie wystarczy już tylko zrobić pętlę obliczającą x1,y1 dla wszystkich x,y i wstawiającą odpowiedni piksel w punkcie x1,y1:
|
1 |
putpixel(x1,y1,ob[x,y]); {ob[x,y] zawiera numery kolorów składające się na obiekt} |
Żeby obiekt obracał się wokół osi innej niż punkt (0,0) należy do x1,y1 dodać współrzędne osi.
Poniższa metoda napisana w Delphi, wykonywana po kliknięciu na przycisku „Button1”, spowoduje wyświetlenie na formie obrazka wczytanego do komponentu „Image2” obróconego o kąt podany w „edit”
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
procedure TForm1.Button1Click(Sender: TObject); var alfa,cosa, sina, sina90, cosa90:real; x,y,x1,y1,ox,oy:integer; begin {pobranie kąta podanego w radianach} alfa:=strtofloat(edit1.text); {wyliczenie potrzebnych funkcji trygonometrycznych, żeby zmniejszyć czas wykonania pętli} cosa:=cos(alfa); sina:=sin(alfa); cosa90:=cos(alfa+pi/2); sina90:=sin(alfa+pi/2); {Zdefiniowanie punktu wokół którego ma odbywać się obrót- w tym przypadku jest to środek obrazka} ox:=image2.Picture.width div 2; oy:=image2.Picture.height div 2; {pętla rysująca} for x:=0 to image2.picture.width-1 do for y:=0 to image2.picture.height-1 do begin {wyliczenie współrzędnych po obrocie} x1:=round(cosa*(x-ox)+cosa90*(y-oy)); y1:=round(sina*(x-ox)+sina90*(y-oy)); {narysowanie na płótnie odpowiedniego pixela} canvas.pixels[x1+60,y1+60]:=image2.picture.bitmap.canvas.pixels[x,y] {60,60 będzie punktem odpowiadającym punktowi znajdującemu się na osi obrotu} end; end; |
Niestety okazuje się, że po obrocie o np.: pi/3 obraz będzie zawierał puste pixele. Wynika to z przyjętych zaokrągleń- zdarza się, że współrzędne 2 pikseli wypadają w tym samym miejscu, a w konsekwencji w innym miejscu tego piksela będzie brakować. Aby rozwiązać ten problem należałoby zamiast pojedyńczego piksela uzupełniać także sąsiedni:
|
1 2 3 |
canvas.pixels[x1+60,y1+60]:=image2.picture.bitmap.canvas.pixels[x,y]; canvas.pixels[x1+61,y1+60]:=image2.picture.bitmap.canvas.pixels[x,y]; |
Dzięki temu, jeżeli sąsiedni piksel z jakiegoś poziomu zostanie pominięty, obrazek nie będzie miał pustych miejsc. Wadą tego rozwiązania jest jednak znacznie spowolnienie algorytmu. Można to nieco poprawić wyliczając kolor, który ma być wstawiony, tylko raz:
|
1 2 3 4 5 |
kolor:=image2.picture.bitmap.canvas.pixels[x,y]; {kolor:tcolor} canvas.pixels[x1+160,y1+160]:=kolor; canvas.pixels[x1+161,y1+160]:=kolor; |
Autor: Piotr Szczepaniec