POCISKI, STRZELANIE… W WARSTWIE- IZOMETRIA W ŚWIECIE PROSTOKĄTNYM- CZEŚĆ 5
Trochę wolnego czasu i jest kolejna część;) tym razem o strzelaniu lub inaczej mówiąc o naturze pocisku. Oczywiście kod programu jak i cały przykład wymaga Delphi i komponentu Omegi. Treść artykułu oraz sam pomysł jest uniwersalny, co nie oznacza, że jest tym jedynym i najlepszym podejściem do problem. Kod programu zawiera unit o nazwie „UnitPociski”. Jest tam zdefiniowana klasa o nazwie tPocisk, która determinuje cechy, właściwości pocisku. Przykład zawiera pocisk- włócznia, którą rzuca człowiek pierwotny- bohater tego świata 2D.
Poniżej atak na maczugę
Przypomnę „klawiszologię” obowiązująca w dołączonym przykładzie:
– klawisze sterujące- „strzałki” to ruch bohatera; strzałka w lewo/ prawo- obrót w lewo/ prawo; strzałka w „górę”/ w „dół” idź na przód / do tyłu
– Shift + strzałka w „górę” – bieg
– przytrzymany klawisz „m”- animacja mowy
– przytrzymany klawisz ”o”- animacja „och”, czy czegoś tam;)
– klawisz ”a”- rzut włócznią
– „Esc” koniec
Natura pocisku to:
1. moment strzału
2. lot
3. trafienie
4. brak trafienia- zasięg
Ad 1.Moment strzału
W tym punkcie musimy odpowiedzieć na pytanie/ kilka pytań
-czy obiekt strzelający w momencie strzału wykonuje animację czy nie?
-czy strzelamy ogniem ciągłym czy pojedynczym?
-czy obiekt strzelający ma niekończący się zapas amunicji?
-kilka innych pytań, które nasuwają się Tobie czytelniku;)
Ja odpowiem na pierwsze dwa podpunkty, reszta to „matematyczne” cechy obiektu strzelającego.
-czy obiekt strzelający w momencie strzału wykonuje animację czy nie?
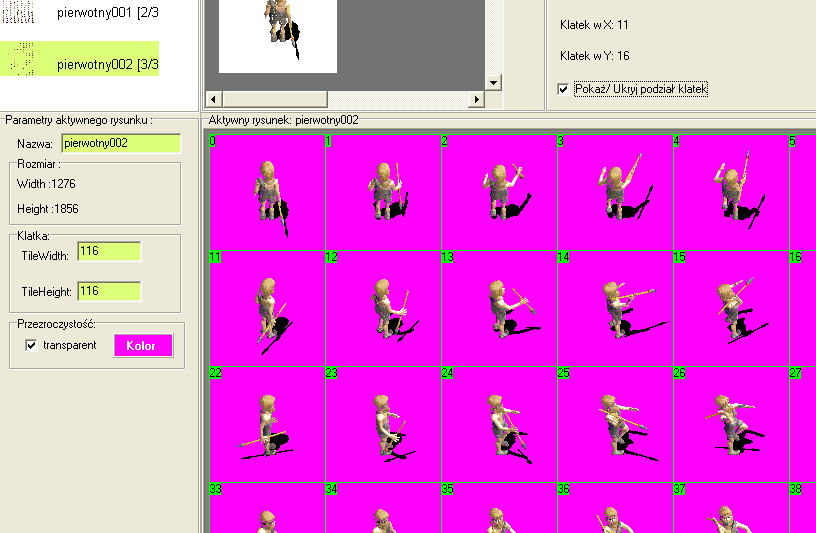
Decydujemy się, że tak. Animacja to kolejne klatki rzucania wybierane odpowiednio do kierunku rzutu.
Tu należy przestrzegać zasady, że raz przyjęta kolejność kierunków stron świata obowiązuje dla wszystkich obiektów i ich klatek rysunków. Ja przyjąłem taką: N, NE, E, SE, S, SW,W, NW
Co w kodzie programu definiuje typ
|
1 2 3 4 5 |
Type tKierunek=(k_N,k_NE,k_E,k_SE,k_S,k_SW,k_W,k_NW); |
W poprzednich częściach opisałem sposób animacji postaci bohatera. Teraz należy na tym samym modelu postępowania dopisać animację rzucania. Pojawią się nowe indeksy klatek
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//wartosci odpowiadaja skrajnym indeksą klatek zachowań tabPierwotny:array[0..49,0..1]of byte= ((0,7),//stoj {0} (8,15),//pauza {1} (16,23),//IDŹ {2} (24,31),// //itd (135,143), {32} //itd (0,10),//rzut dzidą {33} (11,21), (22,32), //itd ); |
oraz procedura związana z rzutem procedure AtakDzida; którą gracz może wywołać wciśnięciem klawisza „a”. Aby mu to umożliwić trzeba to oprogramować, czyli dopisać kolejne zachowania naszego bohatera
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
procedure tPierwotny.Akcja; begin if Stan=stAtak then begin AtakDzida;exit;end; //rzut dzida- klawisz A if(oisButton4{A} in fOmegaInput.keyboard.States) then begin AtakDzida; exit; end; //bieg |
Pasuje opisać, co się dzieje w procedure AtakDzida;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
procedure tPierwotny.AtakDzida; const fLicznikKlatek:integer=0; begin if fLicznikKlatek>10 then begin Stan:=stStop; fLicznikKlatek:=0; //rzucaj dzidą RobPocisk(Form1.OmegaSprite1,Form1.OmegaImageList1,tDzida, Kierunek,X,Y); exit; end; dXAnimacji:=dXAnimacji+deltaSeconds; if dXAnimacji>deltaSeconds*8 then begin inc(fLicznikKlatek); ZmienObraz(tabGrafikiPierwotny[2]); fdxObrazu:=21; fdyObrazu:=14; ImageIndex:=ImageIndex+1; dXAnimacji:=0; Stan:=stAtak; Zachowanie; end; end; |
Jej działanie jest proste i ma na celu przełączanie klatek postaci rzucania gdy tylko zostanie przekroczona ta wartość
|
1 |
if dXAnimacji>deltaSeconds*8 then |
gdzie deltaSeconds to przekazana wartość z zegara gry. Gdy postać wykona pełny cykl klatek rzutu w danym kierunku to można podjąć akcję wyrzucenia pocisku, która równoznaczna jest z utworzeniem jego „duszka”. Od tego momentu pocisk zaczyna żyć i zachowuje się tak jak go opisaliśmy w procedurach jego klasy.
Ten warunek
|
1 |
if fLicznikKlatek>10 then |
decyduje o prędkości “strzelania”- wyrzucania pocisków. Jego brak równoznaczny jest z ogniem ciągłym;)
Ad 2. lot
W tym punkcie to można różne zachowania przypisać lecącemu obiektowi. Ale kilka elementów jest wspólnych dla różnych typów pocisków. Czy to jest dzida, kamień, kula, promień lasera zawsze musimy określić kierunek strzału, wybrać klatki animacji lotu, wykryć trafienie, uśmiercić cel, uśmiercić pocisk itp.
– kierunek lotu
Poniżej możliwe kierunki ruchu obiektów wraz z miarami kata wyrażonymi w stopniach i części dziesiętnej stopnia. 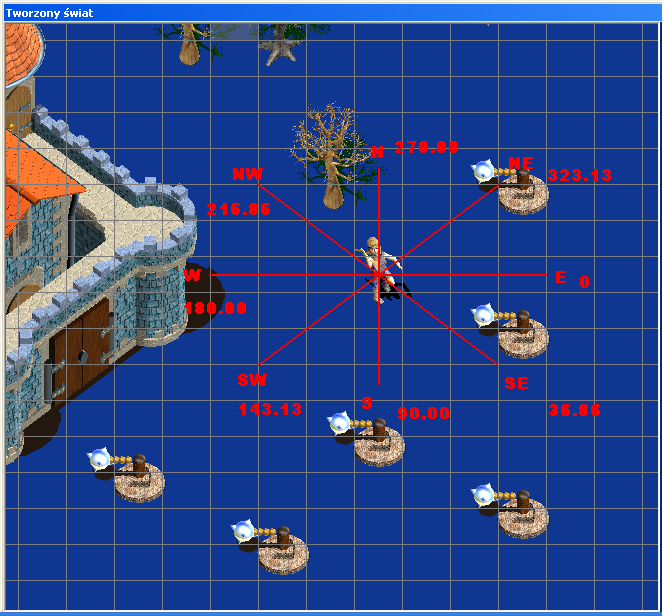
Można zadać pytanie: Dlaczego dla kierunku SE kąt wynosi 36.86stopnia?
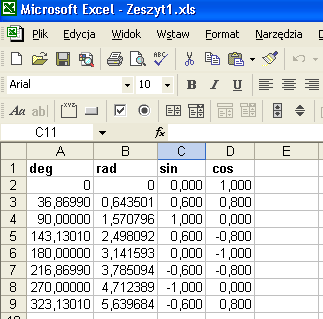
Wartość ta wynika z rozmiaru kostki świata tu wynosi ona 48×36 pikseli czyli tangens kąta kierunku SE to stosunek 36/48 licząc arctg otrzymamy 36.86. Poniżej tabelka z Excela
Pasuje te wartości zapisać w kodzie programu w postaci stałej tablicy. Ale w takiej kolejności jak przyjęliśmy kierunki świata : N, NE, E, SE, S, SW,W, NW
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
const cKaty:array[0..7,0..3]of single= ( (270.00000 ,4.71238898 ,-1.000, 0.000),//N (323.13010 ,5.639684157,-0.600, 0.800),//NE (0 ,0 ,0 , 1), //E (36.86990 ,0.64350115 ,0.600 , 0.800),//SE (90.00000 ,1.570796327,1.000 , 0.000),//S (143.13010 ,2.498091504,0.600 ,-0.800),//SW (180.00000 ,3.141592654,0.000 ,-1.000),//W (216.86990 ,3.785093803,-0.600,-0.800) //NW ); |
Dlaczego pamiętam stopnie, radiany oraz wartość funkcji sinus i cosinus? W tej chwili nie odpowiem na to pytanie – bo sam nie wiem;) Może do czegoś się przydadzą. Wystarczy pamiętać sinus i cosinus. Są one wykorzystane w równaniu ruchu pocisku.
|
1 2 3 |
X:= X+dVx*MoveCount*CosAlfa+SkokX; Y:= Y+dVy*MoveCount*SinAlfa+SkokY; |
Gdzie CosAlfa i SinAlfa to zmienne, którym przypisano wartości funkcji sinus w momencie tworzenia pocisku. Do tych zależności jeszcze wrócę w dalszej części artykułu.
I tu uwag lepiej jest pamiętać raz obliczone wartości sinusów i cosinusów niż je wielokrotnie obliczać w zegarze gry. Szybciej jest pobrać coś z pamięci niż policzyć, a zwłaszcza wartości funkcji trygonometrycznych, a w grze może się zdarzyć, że w danym momencie będzie „latać” kilkadziesiąt pocisków.
Wiemy już, jakie mamy kierunki lotu. Teraz należy ustalić- przypisać ten kierunek do pocisku. Jak to zrobić? Bardzo prosto. O kierunku decyduje kierunek ustawienia strzelającego obiektu – tu postać pierwotniaka. Przypuśćmy, że postać- duszek stoi patrząc w kierunku SW Stosując prosty pomysł wynikający z przyjętego ujednolicenia kolejności kierunków świata dla klatek ruchu, katów itp. przechowywanych w tablicach wystarczy podać go do procedury tworzenia pocisku i odczytać indeks kierunku
|
1 2 3 |
//rzucaj dzidą RobPocisk(Form1.OmegaSprite1,Form1.OmegaImageList1,tDzida,Kierunek,X,Y); |
Dal przypomnienia funkcja Ord()[/] zwraca indeks występowania elementu w zbiorze, czyli
ord(Kierunek) dla Kierunek:=k_SW; da nam ze zdefiniowanego zbioru typów możliwych kierunków
|
1 |
tKierunek=(k_N,k_NE,k_E,k_SE,k_S,k_SW,k_W,k_NW); |
wartość 5. I teraz wszystko odczytujemy z naszych tablic spod indeksu 5. Porządek w organizacji danych ułatwia życie, gdzieś w kodzie programu znajdziesz Czytelniku te linie
|
1 2 3 4 5 6 7 8 |
fAlfa :=ckaty[ord(Kierunek),1]; sinAlfa:=ckaty[ord(Kierunek),2]; cosAlfa:=ckaty[ord(Kierunek),3]; ImageIndex:=cKlatkiPocisku[Ord(typ),Ord(kierunek),0]; |
Wrócę na moment do równań ruchu:
|
1 2 3 |
X:= X+dVx*MoveCount*CosAlfa+SkokX; Y:= Y+dVy*MoveCount*SinAlfa+SkokY; |
Należy pamiętać, aby uwzględnić w nich przesunięcie świata wynikające z ruchu bohatera czy ogólnego przesuwania myszką. Lecący pocisk musi być odpowiednio przesuwany o wartości skoku świata w kierunku osi X i Y. Jeżeli przewidujemy pokazywanie przez jakiś czas obrazu pocisku po jego upadku to też o tym musimy pamiętać. Ale wtedy ich postać będzie prostsza:
|
1 2 3 |
X:= X+SkokX; Y:= Y+SkokY; |
Lecz pocisk musi zliczać głębię w izometrycznym świecie, tu zmienna z. Robię to na tych samych zasadach, co dla duszka postaci, tylko daję je wartość zwiększoną o osiem jednostek. Tak, aby mogła szybować nad drzewami czy dachami. Ale jeżeli już upadnie, to zmniejszam tą wartość, tak, aby postacie mogły sobie deptać po obrazie leżącej na trawie włóczni.
-symulacja lotu
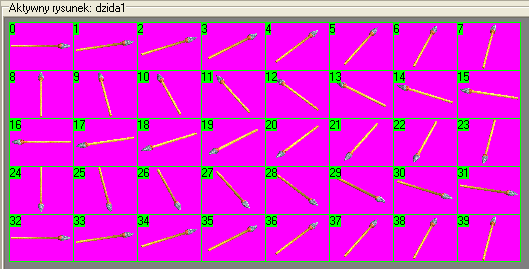
Jest opisana w/w równaniami. I nie są to równania „balistycznej”. Symulację krzywej balistycznej uzyskałem z animacji klatek lecącej dzidy;) Owszem dla strzału z katapulty tak się nie da zrobić- szkoda pamięci na obraz. Pomysł tkwi w klatkach. Poniżej ich obraz
Tworząc tablicę animacji klatek lecącej dzidy dla kolejnych kierunków geograficznych. Powiedzmy o takiej postaci:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
cKlatkiPocisku:array[0..0,0..7,0..8]of byte=( ( (8,8,8,8,8,8,8,8,8), //N (5,4,3,2,1,31,30,29,28), //NE (4,3,2,1,0,31,30,29,28), //E (2,1,31,30,29,28,27,26,25), //SE (24,24,24,24,24,24,24,24,24),//S (15,14,17,18,19,20,21,22,23),//SW (12,13,14,15,16,17,18,19,20),//W (11,12,13,14,15,18,19,20,21) //NW )//dla pocisku klasy tDzida- Ord(tDzida) da indeks 0 ); |
uzyskam symulację krzywej toru lotu pocisku wykonując to w tej procedurze
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
procedure TPocisk.Move(const MoveCount: Single); begin if (fidKafla<0) or (fidKafla>DaneMapy.xCount*DaneMapy.yCount-1) then dead; SmiercZUplywuCzasu(MoveCount); inherited Move(MoveCount); if not fStopAnimacja then begin X:= X+dVx*MoveCount*CosAlfa+SkokX; Y:= Y+dVy*MoveCount*SinAlfa+SkokY; Pozycja(x,y,DaneMApy.W1Kosc,DAneMapy.H1Kosc); dXAnimacji:=dXAnimacji+MoveCount; if dXAnimacji>MoveCount*15 then begin inc(fKlatkaAnimacji); if fKlatkaAnimacji>high(cKlatkiPocisku[Ord(typ),Ord(kierunek)])-1then begin fStopAnimacja:=true; fSmiercZUplywuCzasu:=true; DoCollision:=false; end; ImageIndex:=cKlatkiPocisku[Ord(typ),Ord(kierunek),fKlatkaAnimacji]; dXAnimacji:=0; end; end else begin X:= X+SkokX; Y:= Y+SkokY; Pozycja(x,y,DaneMApy.W1Kosc,DAneMapy.H1Kosc); z:=z-7;//połóż na trawie; end; end; |
Przerzucanie klatek wykonuję na tych samych zasadach, co dla postaci pierwotniaka. Problem tkwi we właściwym doborze klatek ruchu. Ja miałem do dyspozycji gotową grafikę pobrana ze strony wspomnianej w pierwszej części tego cyklu, swoim programikiem- „automatem” posklejałem w kolejne klatki i na „oko” powybierałem. Jest jak jest.
Ad 3. i ad 4.- trafienie / brak trafienia, zasięg
Ten tematy można omówić jako całość. Ogólnie należy wykryć kolizję. W dołączonym przykładzie możemy niszczyć jednym trafieniem włóczni wirujące maczugi. Maczuga ginie, ginąc zwalnia zakazane pole ruchu drogi. Po jakimś czasie ginie pocisk. Jeżeli pocisk nie trafił, to musi skończyć lot i też zginąć po określonym czasie. Długość lotu, czyli zasięg określam bardzo prosto- dojściem do końcowej klatki animacji i wykonania procedury
|
1 |
procedure TPocisk.SmiercZUplywuCzasu(const MoveCount: Single); |
Kolizja jest standardowa procedurą
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
procedure TPocisk.onCollision(const Sprite:Tsprite;const colX,colY:integer); begin if (Sprite is TKostkaMapy)then begin //akcje w mapie świata gry PMapa(Lista.Items[TKostkaMapy(Sprite).idWskMApy])^[TKostkaMapy(Sprite).fIDKafla].idKlatka:=-1; PMapa(Lista.Items[TKostkaMapy(Sprite).idWskMApy])^[TKostkaMapy(Sprite).fIDKafla+ DaneMapy.XCount].RGBA.zakazWstepu:=0; PMapa(Lista.Items[TKostkaMapy(Sprite).idWskMApy])^[TKostkaMapy(Sprite).fIDKafla]. Animacja.fKolizja:=false; TKostkaMapy(Sprite).ZmianaKlatki; //akcje dla pocisku fSmiercZUplywuCzasu:=true; fStopAnimacja:=true; dVx:=0; dVy:=0; DoCollision:=false; end; end; |
Można ją przerobić tak aby reagowała na pozycję grota włóczni. Należy określić zakresy obszaru prostokąt położeni grota w kolejnych klatkach i sprawdzić czy w momencie kolizji te wartości procedury wykrywania kolizji
|
1 |
const colX,colY:integer |
mieszczą się w tych obszarach, ale mnie się już tego nie chciało pisać.
I to by było na tyle
Pozdrawiam Adam Lasko(oksal) Zbylitowska Góra 3 maja 2008
PS
Pliki wymagane do tej części artykułu to:
swiat_512x384.mue2D
kasztan.oil
teren_rosliny.oil
swiatynie.oil
zamki.oil
pierwotny001.oil
wiatrak.oil
mlyn.oil
pociski.oil
D3DX81AB.DLL
MPPSDK.DLL
Autor: oksal