Witam w części drugiej wszystkich zainteresowanych tym tematem. Dla przypomnienia:
z części pierwszej wiemy jak zmienić barwę „duszka” – bohatera jeżeli znajduje się on na obcym obiekcie. Dążymy aby tę umiejętność wykorzystać w przypadku gdy bohater lub inny obiekt żywy naszej gry 2D zmienił „ubarwienie” lub rysunek – obraz (można i tak) jeżeli będzie to obiekty inny niż grunt. Ponadto chcę tu omówić problem chodzenia po lesie bez mamy i taty (jak by w pobliżu była mama lub tato, to by na pewno nie pozwolili nam wejść do lasu bez opieki))
Pytanie dlaczego?
A tylko dla tego, że w lesie można zabłądzić lub spotkać borostwora (to też może być temat do kolejnego artu)…Chyba, że w lesie istnieje sieć dróg….
Inaczej mówiąc: w tej części zajmiemy się błądzeniem po lesie a w trzeciej – przyzwoitym chodzeniem po leśnych drogach.
W jednym i drugim przypadku zawsze nasz bohater może znaleźć się w „cieniu obrazu drzewa” a my chcemy pokazać jego obraz, ale lekko zmieniony – powiedzmy, że w taki sam sposób jak w części pierwszej…
Oprócz zmiany koloru mamy kolejny problem – głębia… Tego problemu nie będzie jeśli rozmiary obiektów umieszczanych w świecie 2D będą dzielone na siatkę klocków o wymiarach siatki warstwy. Stosując taki podział, to przy budowie świata w edytorze naszej gry szlak nas trafi (mnie już trafił jak sobie taki zrobiłem) jeśli będziemy chcieć dodać do mapy budynek czy też drzewo. Po prostu budynek będziemy musieli osadzać po kawałku na siatce mapy i jeśli będziemy próbować za budynek wejść, to się nieźle natrudzimy. Prawdopodobnie kod takiego rozwiązania będzie spowalniać grę. Musimy wymyślić coś innego. Szukamy rozwiązania które:
a). pozwoli osadzać budynki, drzewa itp. w całości,
b). pozwoli zmienić kolor bohatera za takim budynkiem lub drzewem,
c). jeśli będzie to na przykład las, to chcemy chodzić za drzewami – zderzamy się tylko z pniem (ten pomysł może również być do chodzenie za budynkiem a nie za jego dachem).
Problem punkt c jest wynikiem tego, że w świecie płaszczaków nie ma 3 wymiaru, ale my możemy łatwo go zasymulować poprze wprowadzenie głębi. Klasa TSprite i jej pochodne mają oprócz współrzędnej X, Y współrzędną Z. W kraju 2D decyduje ona o kolejności wyświetlania obrazów graficznych . My ją określimy i wykorzystamy inaczej niż w przykładach dołączonych do komponentu OMEGI. Standardowo współrzędna Z dla warstwy podstawowej może mieć wartość 0, dla warstwy kolejnej 1 i tak dalej. Takie podejście nic nam nie da. Choć można odpowiednio sobie przeliczyć głębię na podstawie współrzędnej X i Y. Ale jeszcze raz podkreślam będą, to kolejne dodatkowe obliczenia…
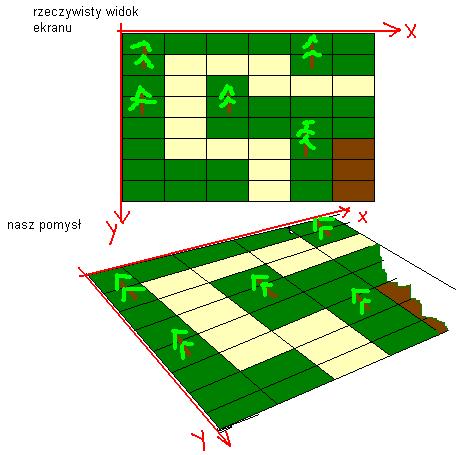
Jak sobie z tym poradzić? Bardzo prosto. Proszę spojrzeć na poniższy rysunek, który przedstawia mapę 2D widzianą na ekranie monitora i drugą poniżej, ustawioną tak jak byśmy patrzyli na szachownicę podczas gry w szachy.
Z takiego spojrzenia na kraj płaszczaków łatwo zauważyć, że kolejne wiersze klocków mapy układają się w pewien sposób. Wiersze o mniejszej współrzędnej ekranowej Y są jakby dalej od nas….Odkryliśmy głębię w krainie 2D
Jak to wykorzystać do naszych pomysłów?
Podczas tworzenia kolejnych warstw świata oprócz zapamiętania współrzędnej X i Y zapamiętamy Z, która będzie mieć dla kolejnych wierszy przypisany na przykład numer wiersza tablicy przechowującej planszę naszej gry. Dodatkowo przyjmujemy losowy dobór drzew które będą pojawiać się w polach tablicy mapy o numerze zero. Oczywiście można sobie przyjąć dużo więcej takich indeksów na różne obiekty lub różne fragmenty klatek. Ale ogólna zasad jest tu przedstawiona. Poniżej odpowiedni wyciąg z kodu części 2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
.................... //tworz mape swiata for w:=0 to high(Warstwa0)do for k:=0 to high(Warstwa0[0])do begin //wartswa gruntu Warstwa0[w,k].x:=k*OmegaImageList1.ImageList.Items[0].TileWidth; Warstwa0[w,k].y:=w*OmegaImageList1.ImageList.Items[0].TileHeight; Warstwa0[w,k].z:=w; //tworz losowo drzewa if MapaWarstwa0[w,k]=0 then begin Roslina.x:=k*OmegaImageList1.ImageList.Items[0].TileWidth+ (OmegaImageList1.ImageList.Items[0].TileWidth-Roslina.Image.TileWidth)div 2+16;//wyjustuj o 16 wzgledem tablicy Drogi; Roslina.y:=w*OmegaImageList1.ImageList.Items[0].TileHeight-(Roslina.Image.TileHeight-OmegaImageList1.ImageList.Items[0].TileHeight); Roslina.z:=w+2;//zwiększ wartość o 2 względem Z gruntu //zapamietaj kolumne i wiersz zaczepienia rosliny Roslina.k:=k; Roslina.w:=w; ..................... |
I teraz jeśli tylko chodzimy po świecie naszym bohaterem wystarczy określić wierzchołek klatki kostki mapy w jakiej się znajduje i na tej podstawie nadawać mu nową wartość Z. Szybkie i proste. Szybkie bo w momencie tworzenia świat określamy Z-ety dla kostek mapy. Proste – bo i tak nie unikniemy w grze określania w jakiej kostce mapy się znajdujemy, a jej numer wiersza jest naszym poszukiwanym ZET :]. Znajomość Z w świecie płaszczaków jest warunkiem aby chodzić wśród drzew lub budynków miasta 2D.
Poniżej fragment procedury określającej numer kolumny , wiersza i Z położenia gracza:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//*******BLOK KLASY GRACZ******************************* procedure TGracz.JakaKostka; begin .. .. .. //policz kol i wiersz w swiecie warstw i wyznacz Z k:=Round(x-Warstwa0[0,0].x+Image.TileWidth div 2)div Warstwa0[0,0].Image.TileWidth; w:=Round(y-Warstwa0[0,0].y+Image.TileHeight div 2)div Warstwa0[0,0].Image.TileHeight; //zabezpiecz przed wyjściem poza rozmiar tablicy if k< 0 then k:=0; if k>19 then k:=19; if w< 0 then w:=0; if w>19 then w:=19; z:=w+3; end; |
Jak chodzić po lesie? Ano tak aby nie uderzać w pnie drzew ;).
Aby efektywnie oprogramować tą informację należy popatrzeć na poniższy rysunek
Czarne prostokąty, to pola kostek gruntu, czerwony, to rozmiar obrazu osadzanego drzewa (podkreślam, że w tym projekcie nie dążymy do dzielenia obrazków na klatki, chcemy obrazy w całości). Jeżeli klasycznie podejdziemy do problemu, to współrzędne lewego rogu czerwonego prostokąta wyznaczą klatkę zaczepienia obiektu w świecie… Ta klatka mapy zostanie zajęta przez czubek drzewa a nie przez jego pień. Musimy wymusić zajęcie klatki odpowiadającej współrzędnym pnia. Należy to zrobić w momencie tworzenia świata. Zobacz kod procedury: TworzSwiat;
Tym prostym sposobem mamy możliwość chodzenia przed jak i za drzewem – czyli być za koroną drzewa. Ale czy to koniec problemu? Otóż nie. A co będzie jeśli w kostce gruntu wyrośnie małe drzewo lub jeszcze mniejszy grzyb? Całe pole zostanie zajęte. Nie zerwiemy grzybka. Nasz duszek nie podejdzie do niego. Bo na przykład nasza kostka gruntu ma rozmiar 64×32, grzyb 16×8 i rośnie w środku…
No już pewnie w tym miejscu mógłbym usłyszeć: Co ty facio gadasz? A od czego jest test kolizji zmiany pikseli? (odpowiedź podana jest w pytaniu)
A tak na poważnie… Proszę zauważyć, że jeśli taki test zmiany pikseli zastosujecie, to nigdy nie napiszecie algorytmu szukania drogi lub dojścia do zadanego punktu. Test pikseli nie będzie wykonywany, jeśli duszek jest poza widoczną częścią ekranu. A takich duszków różnych postaci może być kilka. Postać taka żyje własnym życiem – jest naszym wrogiem lub sprzymierzeńcem. Taki algorytm zawsze wykonywany jest po klatkach mapy. Osoby zainteresowane gotowym przykładem wykonania tego algorytmu wraz z możliwością podglądnięcia jego serca odsyłam do mojego projektu na www.delphi.ilion.pl dział narzędzia.
Wracamy do tematu – kolejnego problemu:
Co zrobić aby podejść do małego drzewka lub grzybka?
Odpowiedź prosta: Zwiększyć precyzję siatki mapy. Można zadać siatkę mapy 32×32 – ale spadnie FPS. Zostajemy przy naszej 64×32 i nie rezygnujemy z pomysłu zwiększenia precyzji siatki.
Jak to najłatwiej zrobić (i tak aby było efektywnie)? Tworzymy nową dynamiczna tablicę takiej siatki (w kodzie programu to tablica: Drogi : array of array of integer;)
Tą tablicę oprzemy na wymiarze 32×32, można też zastosować 16×16. Ale czy jest sens? Jeżeli nasze duszki są szerokości porównywalnej z 16 pikselami to tak. Ale jak nie, to należy tego unikać – pamięć kompa jest ograniczona.
W klatkach tablicy Drogi odwzorujemy współrzędne zaczepienia pni, według poniższego schematu
Dla uproszczenia rysunek przedstawia świat zbudowany z 4 pól i podstawowej klatce mapy 64×64:
Teraz należy odpowiednio przeliczać położenia żywych obiektów na kolumny i wiersze takie tablicy Dróg. I jeśli będzie tam stać indeks obiektu powodującego kolizję, to będzie równoznaczne z barakiem przejścia lub podjęcia jakieś innej akcji.
Technicznie taki odczyt załatwia ta procedura klasy Tgracz
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
procedure TGracz.JakaKostka; begin //policz kol i wiersz w tablicy drog kd:=Round(x-Warstwa0[0,0].x+Image.TileWidth div 2) div 32; wd:=Round(y-Warstwa0[0,0].y+Image.TileHeight div 2) div 32; if kd<0 then kd:=0; if kd>High(Drogi[0]) then kd:=high(drogi[0]); if wd<0 then wd:=0; if wd>High(Drogi) then wd:=high(drogi); //policz kol i wiersz w swiecie warstw i wyznacz Z k:=Round(x-Warstwa0[0,0].x+Image.TileWidth div 2)div Warstwa0[0,0].Image.TileWidth; w:=Round(y-Warstwa0[0,0].y+Image.TileHeight div 2)div Warstwa0[0,0].Image.TileHeight; if k< 0 then k:=0; if k>19 then k:=19; if w< 0 then w:=0; if w>19 then w:=19; z:=w+3; end; |
I jest ona wywołana w procedurze TGracz.MoznaIsc:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
procedure TGracz.MoznaIsc; begin //Sterowanie Graczem stareX:=x; stareY:=y; if oisUp in Form1.OmegaInput1.keyboard.states then//idz do gory SkokY:=SkokY+1; if oisDown in Form1.OmegaInput1.keyboard.states then//idz w dół SkokY:=SkokY-1; if oisRight in Form1.OmegaInput1.keyboard.states then//idz w prawo SkokX:=SkokX-1; if oisLeft in Form1.OmegaInput1.keyboard.states then//idz w lewo SkokX:=SkokX+1; x:=x-SkokX; y:=y-SkokY; JakaKostka; //sprwdz czy mozna byc w nowej pozycji, jak nie to zeruj skok if(Drogi[wd,kd]>-1) then begin SkokX:=0;// SkokY:=0;// end; //ustwa gracza w starej pozycji x:=stareX; y:=stareY; end; |
Koniec części 2
W części 3 wprowadzimy drogi do lasu.
Pozdrawiam oksal
Autor: oksal