Witam, w tym artykule przedstawię algorytm wraz z opisem do wyszukiwania najkrótszej drogi według (prawie) sposobu przytoczonego przez oksala w jego artykule: wyszukiwanie drogi oksala. Jednak ja rozszerzyłem swój algorytm o pewną bardzo przydatną cechę, której brak w oksalowym algorytmie – wybieranie tego z najbliższych celowi miejsc, gdy ten jest nieosiągalny, do którego droga od miejsca startu jest najkrótsza. Może się to wydawać w tej chwili niezrozumiałe, w dalszej części wyjaśnię ten problem dokładnie.
Mój algorytm działa na tablicy dwuwymiarowej i kolejce, wyniki czasowe są moim zdaniem zadowalające i są mniej więcej podobne do tych osiąganych za pomocą algorytmu oksala:
mapa 256 kafli na 256 – około 25ms,
512 na 512 – około 150ms,
1024 na 1024 – około 600ms.
Dwa ostatnie są trochę gorsze niż te oksalowe, ale on nie wliczał czasu potrzebnego na utworzenie i wypełnienie tablicy mapy, a to „trochę” trwa 😉
Opis algorytmu.
Przytoczę ten opis z artykułu oksala:
Autor książki „Algorytmy,” Maciej Sysło:
Dane: Labirynt (u nas mapa świata 2D, czyli prostokąt z jednym wyjściem, wypełniony ścianami, które są równoległe do zewnętrznych ścian i nie tworzą zamkniętych obszarów). Dany jest punkt w polu s (nasz punkt startu).
Wynik: Droga w labiryncie, która prowadzi z pola s do wyjścia.
Krok 0: Przyjmij, ze na początku nie byłeś w żadnym polu labiryntu, a więc wszystkie pola są nieodwiedzone.
Krok 1: Umieść w kolejce Q pole s. W polu s umieść liczbę 0 (zero).
Krok 2: Dopóki kolejka Q nie jest pusta wykonuj kroki 3 – 5.
Krok 3: Usuń z kolejki Q jej pierwszy element – oznaczmy to pole przez v.
Krok 4: Dla każdego pola w sąsiedniego względem v i nieoddzielonego od niego ścianą wykonaj krok 5.
Krok 5: Jeśli nie byłeś jeszcze w polu w, to umieść w nim liczbę o jeden większą od liczby znajdującej się w polu v. Jeśli pole w zawiera wyjście to przejdź do kroku 6, a w przeciwnym razie dołącz w do końca kolejki Q.
Krok 6: (W tym kroku budujemy od końca listę pól tworzących najkrótszą drogę z pola s do pola w, na którym zakończył działanie krok 5). Dopóki wnie jest polem s, wykonuj: za kolejne (od końca) pole drogi przyjmij w i za nową wartość w przyjmij pole sąsiednie względem w, w którym znajduje się liczba o jeden mniejsza od liczby znajdującej się w obecnym polu w.
Ten algorytm nie uwzględnia sytuacji, kiedy pole docelowe jest nieosiągalne, np. jest za murem, lecz my temu zaradzimy, ale na razie, żeby ułatwić zrozumienie, przedstawię działanie powyżej opisanego algorytmu na przykładzie wraz z grafiką mapy. Mapa ma wymiar tylko 4 kafle na 4, ale po co większa skoro i na takiej możemy zadziałać :).
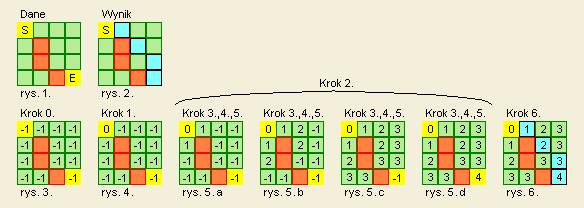
Na pierwszym rysunku przedstawiona jest mapa, a na drugim – jak widać – wynik działania algorytmu, czyli znaleziona droga. Zielone pola to wolne przejścia, a pomarańczowe to mury. Idziemy od pola S do E.
Krok 0.
Wszystkie pola tablicy wypełniamy wartością nieodwiedzone, za którą ja przyjąłem -1, co widać na rysunku trzecim.
Krok 1.
Polu startowemu nadajemy wartość 0 (rysunek czwarty), a następnie dodajemy je do kolejki Q.
Krok 2.
Drugi krok to pętla wykonująca się tak długo, aż zwiedzimy całą mapy i/lub dojdziemy celu. W pętli tej kolejno wykonujemy Kroki: 3., 4. oraz 5..
Krok 3.
Przypisujemy zmiennej pomocniczej v współrzędne pierwszego elementu kolejki Q a potem ten element z niej usuwamy.
Krok 4.
Z każdeym polem w na około v wykonujemy Krok 5., o ile pole: to nie jest murem, nie wychodzi poza mapę oraz nie było jeszcze odwiedzone.
Krok 5.
Teraz przyda się spojrzeć na rysunek 5 a. Każdemu polu w na około pola aktualnie rozpatrywanego (a rozpatrujemy teraz akurat pole startowe, bo dopiero rozpoczął działanie nasz algorytm) przypisywana jest wartość o jeden większa niż znajduje się pod polem v (w tym przypadku 1). Następnie dodajemy te punkty, którym właśnie nadaliśmy wartość, do kolejki Q (każdy kolejny dodajemy na jej koniec). Popatrzcie na rysunki 5 a – d, mapa wypełnia się wartościami.
Pętla nie wykonuje się tylko 4 razy, ale więcej, bo więcej jest pól do „okrążenia”, pominąłem kilka, chciałem tylko zobrazować jak wygląda mapa z wartościami.
Na koniec obiegu pętli sprawdzamy, czy pole, któremu aktualnie nadawaliśmy wartość nie jest polem docelowym, jeśli tak – przechodzimy do Kroku 6., a po nim przerywamy naszą pętlę.
Krok 6.
Jest to ostatni etap naszego algorytmu, w którym budujemy naszą drogą od końca, więc potem należy jeszcze odwrócić tablicę z kolejnymi punktami drogi. Rozpoczynając ten etap, punktowi pomocniczemu w przypisujemy współrzędne punktu docelowego, a następnie dodajemy do tablicy z drogą na początek punkt w. Teraz uruchamiamy pętlę, która wykonuje się póki ten punkt pomocniczy w nie będzie miał współrzędnych miejsca startu. „Okrążamy” ten punkt pomocniczy i wybieramy pierwsze pole, które ma wartość o jeden mniejszą od wartości pod w, następnie przypisujemy punktowi w współrzędnego tego właśnie znalezionego punktu i dodajemy go do tablicy drogi (na koniec). Spójrzcie na rysunek, zaczynamy z pola końcowego (jest na nim wartość 4), potem przeskakuje na pole obok z wartością 3, potem 2, 1 i docieramy do punktu startowego. Pozostaje nam odwrócić tablicę z punktami drogi i oto – mamy gotową drogę z punktu S do E 🙂
Miejsce docelowe jest nieosiągalne?
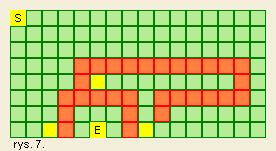
Ten algorytm, o czym już dwa razy chyba wspomniałem, nie uwzględnia sytuacji, gdy pole docelowe jest nieosiągalne (będzie o tym świadczyć to, że na koniec algorytmu tablica z punktami drogi będzie pusta). Nie trudno będzie go rozszerzyć o tę cechę. Dumałem nad tym algorytmem bawiąc się programem oksala i doszedłem do wniosku: co, jeżeli od miejsca docelowego są równo oddalone np. trzy punkty? Który z nich wybrać? Zrobić to losowo? Otóż nie – należy wybrać ten z nich, do którego droga z miejsca startu będzie najkrótsza, spójrzcie na obrazek:
W tym przypadku pola oznaczone na żółto są równo oddalone od pola docelowego E. Najbliżej startu położone jest pole na północ od pola E, ale droga do niego nie jest wcale najkrótsza (wręcz przeciwnie). Dlatego algorytm powinien wybrać pole położone na zachód:
Podam teraz swoje rozwiązanie tego problemu. Mamy do dyspozycji tablicę punktów. W pętli sprawdzamy wszystkie pola mapy – jeżeli dane pole było odwiedzone, to wykonujemy jedno z poniższych:
– jeżeli tablica z punktami jest pusta – dodajemy do niej aktualnie rozpatrywany punkt,
– jeżeli punkty w tablicy są tak samo oddalone jak aktualnie rozpatrywany punkt – dodajemy go na koniec,
– jeżeli punkty w tablicy są położone dalej – usuwamy wszystkie punkty z tablicy i dodajemy do niej aktualny punkt.
W wyniku otrzymamy tablicę z dostępnymi, położonymi najbliżej celu polami. Teraz wystarczy tylko utworzyć drogę od każdego z tych miejsc (tak jak w Kroku 6.) do pola startowego i wybrać ten z punktów, od którego droga będzie najkrótsza.
Implementacja algorytmu.
Ja napisałem ten algorytm w C++ (załącznik do pobrania na dole artykułu).
Na początek definiujemy tablicę, której używać będziemy do „okrążania” pól na mapie. Od tej tablicy zależy, czy umożliwimy poruszanie się w mapie w czterech czy ośmiu kierunkach:
|
1 2 |
const DIRECTIONS_COUNT = 8; // ilość elementów tablicy z kierunkami const SPoint nearPoints[DIRECTIONS_COUNT] = {SPoint(0, -1), SPoint(1, 0), SPoint(0, 1), SPoint(-1, 0), SPoint(-1, -1), SPoint(1, -1), SPoint(1, 1), SPoint(-1, 1)}; |
Kierunki to kolejno: północ, wschód, południe, zachód a kolejne cztery to kierunki na skos.
Jeszcze kilka typów, które zdefiniowałem do pracy z tym algorytmem:
|
1 2 3 4 5 |
struct SPoint { int X, Y; // reszte pomijam, spójrzcie w kod z załącznika }; |
Struktura przechowująca współrzędne.
|
1 2 3 4 5 |
struct SExtPoint : public SPoint { int lengthToEndPoint; // reszte pomijam }; |
Ta struktura przechowuje dodatkowo odległość danego punktu od miejsca docelowego.
|
1 2 3 |
typedef std::vector<int> TMapRow ; typedef std::vector<TMapRow> TMap; typedef std::vector<SPoint> TWay; |
Tutaj kolejno: rząd kafli na mapie, mapa – tablica dwuwymiarowa oraz tablica z punktami drogi.
|
1 2 3 4 5 6 7 8 9 |
class CMap { public: TMap map; SPoint mapSize; // rozmiar całej mapy (jednostka to kafle) SPoint startPos, endPos; // pozycje startowego i docelowego kafla void Resize(int newWidth, int newHeight); // reszte pomijam }; |
Ta klasa przechowuje informację o kaflach mapy (w polu map typu TMap), rozmiar mapy oraz współrzędne kafla startowego i docelowego (wczytujemy je razem z mapą) – te dwa punkty będziemy przysyłać do metody obiektu klasy CFindWayMap. Klasa CMap ma też kilka metod potrzebnych do działania przykładowego programu.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class CFindWayMap : public CMap { private: std::queue<SPoint> Q; TWay bufWay; void PrepareMap(); void CreateWay(TWay *way, SPoint endPos); bool IsPointOutOfMap(SPoint point); public: void FindWay(SPoint startPoint, SPoint endPoint, TWay *way, const TMap &aMap); CFindWayMap(); ~CFindWayMap(); }; |
To klasa, która nas interesuje najbardziej – ma ona za zadanie wyszukiwać drogę w przesłanym obiekcie TMap. Mogłem zrobić wszystko w jednej klasie, ale jakoś postanowiłem to rozdzielić żeby oddzielić wszystko co potrzebne do wyszukiwania drogi. Q to nasza kolejka, znana z opisu algorytmu. bufWay to pomocnicza tablica z drogą. O metodach za chwilę, wspomnę jeszcze o jednej sprawie: w klasie CMap pole map jest używane do przechowywania informacji o rodzajach kafli, natomiast w polu map klasy CFindWayMap umieszczamy kolejne liczby podczas wyszukiwania drogi (spójrzcie na rysunki 3 – 6, wartości liczbowe, które widzicie, są umieszczane właśnie w polu map klasy CFindWayMap).
Czas na metody.
PrepareMap – przypisuje wszystkim polom map wartość nieodwiedzony, co u mnie w programie oznacza wartość -1 oraz czyści pomocniczą tablicę drogi.
|
1 2 3 4 5 6 7 |
void CFindWayMap::PrepareMap() { for (int i = 0; i < mapSize.Y; i++) for (int j = 0; j < mapSize.X; j++) map[i][j] = UNSEEN_FIELD; bufWay.clear(); } |
IsPointOutOfMap – zwraca prawdę, jeśli przesłany punkt wychodzi poza mapę.
|
1 2 3 4 5 |
bool CFindWayMap::IsPointOutOfMap(SPoint point) { if ((point.X < 0) || (point.X >= mapSize.X) || (point.Y < 0) || (point.Y >= mapSize.Y)) return true; return false; } |
CreateWay – ta funkcja ma zadanie wykonać Krok 6. algorytmu – znajduje drogę z pola docelowego do startu i umieszcza ją w przesłanej przez wskaźnik tablicy drogi.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
void CFindWayMap::CreateWay(TWay *way, SPoint actualEndPos) { TWay retWay; SPoint nextW; // dopóki rozpatrywany punkt nie jest pole startowym wykonujemy: while (actualEndPos != startPos) { // - dodajemy aktualnie znaleziony punkt do pomocniczej tablicy drogi retWay.push_back(actualEndPos); // - okrążamy go w poniższej pętli, szukając pola, // która ma wartość o 1 mniejszą niż actualEndPos for (int i = 0; i < DIRECTIONS_COUNT; i++) { nextW.X = actualEndPos.X + nearPoints[i].X; nextW.Y = actualEndPos.Y + nearPoints[i].Y; if (IsPointOutOfMap(nextW)) continue; if (map[nextW.Y][nextW.X] == map[actualEndPos.Y][actualEndPos.X] - 1) { actualEndPos = nextW; break; } } } // poniższy if jest dodatkiem usprawniającym algorytm // jeżeli punkt docelowy jest nieosiągalny if (((*way).size() > retWay.size()) || ((*way).size() == 0)) (*way) = retWay; } |
Po co nam parametr actualEndPos, skoro przechowujemy współrzędne pola docelowego w polu klasy o nazwie endPos? Na końcu znajduje się także pewien warunek – o obu sprawach wspomnę po omówieniu metody FindWay.
Główna funkcja, która wyszukuje drogę – FindWay przyjmuje 4 parametry:
– pozycja startowa,
– pozycja końcowa,
– wskaźnik do tablicy z punktami drogi TWay – po powrocie z funkcji będzie ona wypełniona punktami drogi,
– wskaźnik do mapy, abyśmy mogli sprawdzać czy dane pole jest murem lub czy jest wolne,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
void CFindWayMap::FindWay(SPoint startPoint, SPoint endPoint, TWay *way, const TMap &aMap) { startPos = startPoint; endPos = endPoint; if (startPos == endPos) return; Resize(aMap[0].size(), aMap.size()); PrepareMap(); // krok 0. - wszystkim polom przypisywana jest wartość FIELD_UNSEEN = -1 SPoint v, w; Q.push(startPos); // krok 1. map[startPos.Y][startPos.X] = 0; // krok 1. while (!Q.empty()) // krok 2. { v = Q.front(); // krok 3. Q.pop(); for (int i = 0; i < DIRECTIONS_COUNT; i++) // krok 4 - okrążamy kolejne pola v { w.X = v.X + nearPoints[i].X; w.Y = v.Y + nearPoints[i].Y; if (IsPointOutOfMap(w)) continue; // krok 5. - jeśli pole nie jest ścianą i jeszcze go nie odwiedziliśmy, to: // - nadajemy mu wartość o jeden większą niż posiada pole v // - dodajemy pole w na koniec kolejki if ((aMap[w.Y][w.X] != mtWall) && (map[w.Y][w.X] == UNSEEN_FIELD)) { //if ((nearPoints.X == 0) || (nearPoints.Y == 0) || ((aMap[v.Y + nearPoints.Y][v.X] == 0) && (aMap[v.Y][v.X + nearPoints.X] == 0))) //{ map[w.Y][w.X] = map[v.Y][v.X] + 1; Q.push(w); //} } if ((w.X == endPos.X) && (w.Y == endPos.Y)) { CreateWay(&bufWay, w); // krok 6. - doszliśmy do końca, tworzymy drogę goto wayFound; } } } wayFound: // tutaj zaczyna się część wymyślona przeze mnie // nie znaleziono drogi, tzn., że punkt docelowy jest np. ograniczony murem // musimy znaleźć punkty najbliżej oddalone od celu, do których możemy dotrzeć, // i wybrać ten, do którego droga jest najkrótsza if (bufWay.size() == 0) { std::vector<SExtPoint> closestAvailablePoints; int distance; // sprawdzamy wszystkie pola i jeżeli: for (int i = mapSize.Y - 1; i >= 0; i--) for (int j = mapSize.X -1; j >= 0; j--) { if ((aMap[i][j] != 0) || (map[i][j] == UNSEEN_FIELD) || ((j == endPos.X) && (i == endPos.Y))) continue; distance = abs(endPos.X - j) + abs(endPos.Y - i); // tablica z punktami jest pusta - dodajemy do niej aktualnie rozpatrywany punkt, if (closestAvailablePoints.size() == 0) closestAvailablePoints.push_back(SExtPoint(j, i, distance)); else { // punkty w tablicy są tak samo oddalone jak aktualnie rozpatrywany punkt - dodajemy go na koniec, if (distance == closestAvailablePoints[0].lengthToEndPoint) closestAvailablePoints.push_back(SExtPoint(j, i, distance)); else if (distance < closestAvailablePoints[0].lengthToEndPoint) { // punkty w tablicy są położone dalej - usuwamy wszystkie punkty z tablicy i dodajemy do niej aktualny punkt. closestAvailablePoints.clear(); closestAvailablePoints.push_back(SExtPoint(j, i, distance)); } } } // wywołujemy funkcję CreateWay dla każdego ze znalezionych punktów for (int i = 0; i < closestAvailablePoints.size(); i++) CreateWay(&bufWay, closestAvailablePoints[i]); } // teraz wypełniamy przesłaną tablicę drogi punktami znajdującymi się w pomocniczej // tablicy drogi, z tym, że punkty pobieramy od końca (bo droga była tworzona od końca) for (std::vector<SPoint>::reverse_iterator it = bufWay.rbegin(); it != bufWay.rend(); it++) (*way).push_back(*it); } |
To już koniec algorytmu, ale do wyjaśnienia są jeszcze dwie sprawy. Użyłem raz instrukcji goto, wielu osobom może się to nie spodobać ale wg mnie używanie jej do wyskakiwania z zagnieżdżonych pętli do dobry pomysł.
Jak widzicie, w Kroku 5. daje się zauważyć zakomentowany warunek:
|
1 |
//if ((nearPoints.X == 0) || (nearPoints.Y == 0) || ((aMap[v.Y + nearPoints.Y][v.X] == 0) && (aMap[v.Y][v.X + nearPoints.X] == 0))) |
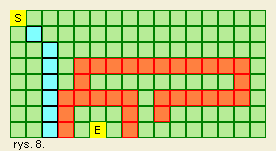
Służy on temu, aby droga nie biegła na ukos, jeżeli pola w pionie i poziomie nie są puste, spójrzcie na rysunek:
Algorytm generuje drogą przedstawioną na rysunku 9 gdy ten warunek jest zakomentowany, natomiast prawdopodobnie jednostka w grze nie mogłaby się przecisnąć między murami – dzięki odkomentowaniu tego kodu droga będzie taka, jak na rysunku 10.
Ostatnia sprawa: warunek na końcu metody CreateWay i parametr actualEndPos. Metoda ta jest tak napisana, aby wyszukiwała drogę z pola actualEndPos do pola startowego. Na końcu warunek ma za zadanie przypisać przesłanej tablicy drogi punkty drogi tylko wtedy, gdy ta przesłana tablica jest pusta lub droga w niej zawarta jest dłuższa niż aktualnie wygenerowana. Wszystko to aby ułatwić sobie życie, gdy punkt docelowy jest nieosiągalny, pisałem już o tym: po znalezieniu punktów równo oddalonych od celu wybieramy ten z nich, do którego droga jest najkrótsza. I teraz każemy w pętli znaleźć drogę do każdego z nich. Jeżeli wyszukana właśnie droga jest krótsza od wyszukanej przed chwilą, to ją przypisujemy do przesłanej w argumencie tablicy drogi, jeśli nie – metoda kończy działanie.
To byłoby na tyle jeśli chodzi o algorytm wyszukiwania drogi, mam nadzieję, że wszystko jest zrozumiałe, zapraszam do ściągania kodu źródłowego, o którym teraz pare słów.
Znajduje się w nim trochę więcej plików, bo musiałem zrobić prosty szablon w DirectX żeby było rysowanie itp. Projekt jest pod Visual C++ 2003. W main.cpp w funkcji CreateObjects (jest na początku pliku) tworzona jest mapa, możecie albo wczytać ją z pliku albo kazać wygenerować. Na końcu tegoż unitu jest wywołanie wyszukiwania drogi. W findway_algo.cpp i h znajdziecie wszystko co najważniejsze.
Do kodu dołączam zbiór grafik – małe i większe, w zależności od tego jakie mapy będziecie chcieli testować oraz kilka przykładowych map.
Jeżeli znajdziecie jakieś błędy albo macie pomysły jak usprawnić algorytm – piszcie na maila: pk@unit1.pl lub wysyłajcie PW na forum.