GIGANTY ŚWIATA 2D część 3
MODEL ŚWIATA IZOMETRYCZNEGO
No i jesteśmy już przy ostatniej części rozważań o istocie ŚWIATÓW… W tej części opiszę jak zrobić GIGANTYCZNY ŚWIAT zbudowany na mapie izometrycznej. Poniżej widok na fragment giganta izometrycznego. Kafli jest 2500 x 2500…
Graficznie nic ciekawego ale z punktu widzenia oprogramowania i rozwiązania problemu sytuacja jest inna. Model ruchu świata jaki tu wykorzystałem jest o wiele precyzyjniejszy niż w innych artykułach opisujących poruszanie światem izometrycznym. W moim rozwiązaniu można kaflem poruszać z dokładnością do jednego piksela a nie do połowy jego szerokości i wysokości… Ten kto czytał inne arty na ten temat wie co mam na myśli.
Układ kafli w świecie izometrycznym
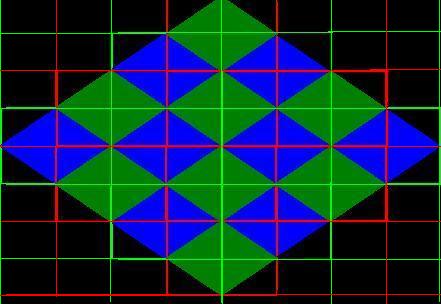
…różni się od prostokątnego. Proszę spojrzeć na poniższy rysunek
Rysunek ten przedstawia standardowe podejście do map izometrycznych. Ale można też to samo przedstawić tak
Robimy więcej kafli, a to pozwoli nam świat izometryczny zamknąć w układzie prostokątnym. Z części drugiej wiemy jak tworzyć giganty i nimi poruszać. Model jest gotowy. Wystarczy go zastosować do układu izometrycznego. Proste.
Mała uwaga w układzie izometrycznym mamy więcej wierszy, które układają się jak na poniższym rysunku
Faza 1 pokazuje stan wyjściowy. Faza druga ma miejsce gdy kości dojdą do momentu przerzucania obrazu (opis: patrz część pierwsza i druga). Ponadto w momencie tworzenia kości warstw należy co drugi wiersz przesunąć w prawo lub w lewo o połowę szerokości. Każdy nowy wiersz jest obniżony w stosunku do poprzedniego o połowę wysokości kafla. W układzie prostokątnym przesunięć nie było a każdy kolejny wiersz był obniżany o całą wysokość kafla.
Co dalej?
Na pewno należy obsłużyć kliknięcie w kafel. Podejście jest bardzo podobne co w układzie prostokątnym z mała różnicą. Mamy do dyspozycji jedną czwartą obszaru kafla. Konkretnie ćwiartkę leżącą przy górnym lewym rogu kafla.
Dlaczego tak jest?
Otóż kafle są tak samo tworzone na „stercie” pamięci jak byśmy układali karty do gry w kolejnych rzędach i wierszach. Przesuwając co drugi wiersz o połowę szerokości karty w prawo lub lewo i obniżając w stosunku do poprzedniego wiersza o połowę wysokości w dół. Jeżeli teraz palcem wskażemy konkretną kartę to możemy dotknąć ją w jednej czwartej powierzchni. Oczywiście ostatni karta może być dotykana w całym obszarze.
Niezależnie od tego czy jest to świat prostokątny czy izometryczny musimy odczytać pozycję w świecie. W moim modelu tę informację przechowuje to pole:
|
1 2 3 4 5 |
TKostkaMapy=class(TSimpleAnimSprite) .... indeks:integer; |
Jego wartość jest odpowiednio zmieniana w procedurze
|
1 |
procedure TKostkaMapy.ZmianaKlatki; |
Wcześniej o tym nie pisałem ale dobrze jest pamiętać kilka informacji o przesuniętym świecie. Ja to przechowuję w tym rekordzie
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
RogSwiata:record x, y:single;//wspolrzedne lewego gornego rogu kolumna, wiersz, Indeks:LongInt;//Indeks Klatki lewego górnego rogu end; |
Takie dane mogą się przydać przy ruchu „automatów”
I to by było tyle o GIGANTACH.
Pozdrawiam oksal Zbylitowska Góra 17.01.2006