W świecie 2D żył starzec, który umiał chodzić po górach i dolinach swego świata, bo znał Talesa z Miletu. W młodości nie chodził do gimnazjum lecz do ośmioletniej podstawówki, tam (ponoć:-) poznał Talesa…
Można powiedzieć, że problem wędrowania po górach i dolinach rozwiązał nam Tales. Czyli aby wyznaczyć względną wysokość w zdeformowanym kaflu świata 2D nie musimy znać:
• równania płaszczyzny zdeformowanego kafla
• wektora kierunkowego takiej płaszczyzny
• płaszczyzna jest wyznaczona 3 punktami, my mamy 4 punkty- rogi kafla
Odpada wyznaczanie równań takich płaszczyzn dla każdego kafla. Względną wysokość można śledzić znając matematykę na poziomie podstawowym, ale zanim podam mój model rozwiązania chciałbym przedstawić podstawowe założenia jakie musi spełniać nasz duszek dla tej części artykułu:
a) kryje się za górami
b) wchodzi na szczyty, potrafi zejść w doliny
c) będąc na szczycie lub w dolinie pozycja musi być prawidłowo odwzorowana w siatce mapy 2D
Warunek a, to odpowiednia modyfikacja kolejności wyświetlania obrazu duszka. Najłatwiej jest zastosować model głębi świata 2D opisany prze zemnie w cyklu artykułów Wędrowanie w świecie 2D. Czyli zmienną Z naszego duszka powiążemy z wierszem świata 2D. W taki sam sposób jak to zrobiliśmy z kaflami w części drugiej tego cyklu artów.
Warunek b wymaga od nas zbudowania takiej funkcji lub procedury, która będzie rozwiązywać problem na kształt zadania z geometrii. W tym miejscu chciałbym podkreślić, że warunek b należy wykonywać tylko w tedy gdy duszek jest w części widocznej świata. Jeżeli jest poza ekranem to należy go pominąć. Znajomość względnej wysokości jest tylko wizualnym efektem. Nie decyduje na przykład o kolizji. W tym przykładzie ja tego nie przestrzegam…Mój druid nie ucieknie poza ekran:-)
Jak obliczyć względną wysokość w zdeformowanym kaflu?
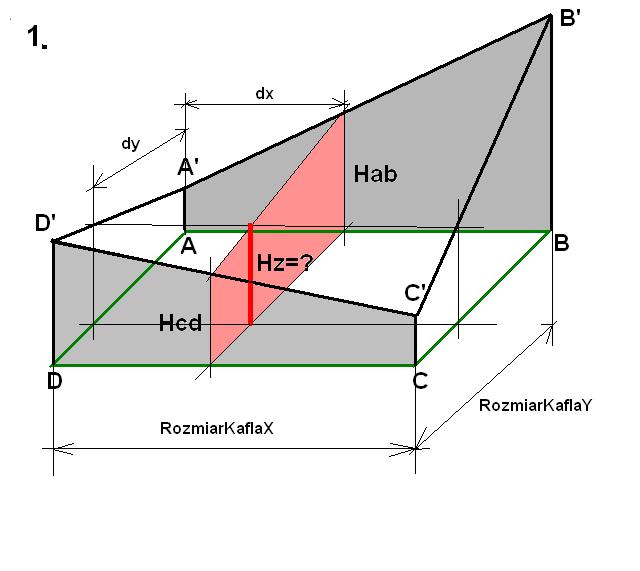
Należy na bieżąco rozwiązywać taki oto problem przedstawiony poniższym rysunkiem:
Problem polega na wyznaczeniu wartości Hab, Hcd na podstawie których wyliczymy Hz. AA’, BB’, CC’, DD’ to znane wartości współrzędnej Y rogów kafla przechowywanych odpowiednio w
|
1 2 3 4 5 6 7 |
PKafel(ListaKafli.Items[fid])^.fA.y PKafel(ListaKafli.Items[fid])^.fB.y PKafel(ListaKafli.Items[fid])^.fC.y PKafel(ListaKafli.Items[fid])^.fD.y |
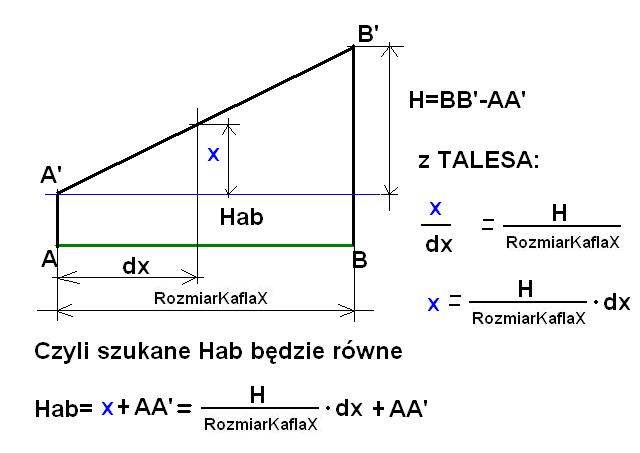
Szukane wartości wysokości Hab i Hcd wyznaczymy na tej samej zasadzie, co pozwoli nam w kodzie programu zastosować jednej i tej samej funkcji. Wysokość Hz wyliczymy inną funkcją, ale matematycznie będzie to ta sama zasado co dla poprzednich dwóch wysokości. Poniżej rysunkiem zobrazuję idee rozwiązania, która polega na tym, że ewentualne trapezy sprowadzamy do trójkąta, wyznaczamy wysokości odpowiadające wartością względnego położenia duszka do górnego lewego rogu kafla (róg A). Czyli musimy znać dx i dy Do znalezionej wartości dodajemy odcinek o który pomniejszyliśmy trapez aby uzyskać trójkąt. Brzmi trochę skomplikowanie. Proszę mi wierzyć rachunek jest prosty. Nawet bardzo prosty
Może teraz pojawić się pytanie: A co by było gdyby AA’ było większe od BB’? Odpowiadam nic. Rachunek naszej funkcji będzie wykonywany tak samo tylko należy pamiętać o właściwej kolejności podawani parametrów do ciała tej funkcji. Znak wyniku będzie uwzględniony poprawnie. Jak by nie było te stosunki są wartościami funkcji tangens….Ale zostawmy to. W podobny sposób wyznaczymy pozostałe wysokości to jest Hcd no i tę właściwą Hz
W kodzie programu będzie to banalna sprawa. Proszę spojrzeć poniżej:
Ta odpowiada obliczeniu Hab i Hcd
|
1 2 3 4 5 6 7 |
function _Hx(h1,h2,dx,RozmiarKaflaX:single):single; begin result:=dx*(h2-h1)/RozmiarKaflaX+h1; end; |
a ta obliczeniu Hz ( zgodnie z oznaczeniami rysunku pierwszego)
|
1 2 3 4 5 6 7 |
function _Hy(h1,h2,dy,RozmiarKaflaY:single):single; begin result:=dy*(h2-h1)/RozmiarKaflaY+h1; end; |
Jedynie teraz musimy znać odległość duszka od górnego lewego rogu kafla w którym się nasz duszek znajduje. W programie zrobimy to tak
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
function TDuszek.Hz:double; var dx,dy:double; begin dx:=(x+Image.TileWidth div 2)-fKolumna*fRozmiarKaflaX; dy:=(y+Image.TileHeight)-fWiersz*fRozmiarKaflaY; result:=_Hy(_Hx(fdHA,fdHB,dx,fRozmiarKaflaX),_Hx(fdHD,fdHC,dx,fRozmiarKaflaX),dy,fRozmiarKaflaY); end; |
W procedurze Move na bieżąco określamy kolumnę i wiersz bycia duszka w świecie 2D oraz odczytujemy parametry rzeźby terenu właściwe dla danego kafla
Warunek c: Jak wyświetlić duszka nie tracąc kontroli nad siatka mapy 2D?
Sprawa jest bardzo prosta. Proszę spojrzeć poniżej
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
procedure TDuszek.Draw; begin //odejmujemy 68 pikseli bo stopy Druida są na tej linii pikseli //zwiększa to realnośc chodzenia po Górach i Dolinach //uniwersalne podejście to odjęcie wysokości klatki czyli //wartość zapisana w Image.TileHeight Image.Draw(Round(x),Round(Hz-68),ImageIndex,0); end; |
Nie używamy zmiennej y Ona służy nam do prawidłowego odczytu położenia duszka w świecie 2D. I tu jeszcze jedna uwaga. Często na forum w podawanych pytaniach (projektach forumowiczów) są używane procedury Draw osobno dla różnych duszków. Proszę pamiętać jeżeli duszek jest potomkiem klasy TSprite, to nie należy tego robić. Bezwiedni nasz duszek jest wyświetlany dwa razy.
Proszę sprawdzić. Wystarczy, że w omawianym przykładzie zmodyfikujesz procedurę Draw na
|
1 2 3 4 5 6 7 8 9 |
procedure TDuszek.Draw; begin inherited; Image.Draw(Round(x),Round(Hz-68),ImageIndex,0); end; |
I to tyle. Teraz wystarczy odpalić program, stworzyć góry i doliny i przy pomocy klawiszy strzałek pochodzić duszkiem DRUIDA w świecie 2D. Spacja pokazuje linie siatki lub je ukrywa.
Pozdrawiam oksal Zbylitowska Góra 3.08.2006
Autor: oksal